12 As A Fraction In Simplest Form

Quick Links :

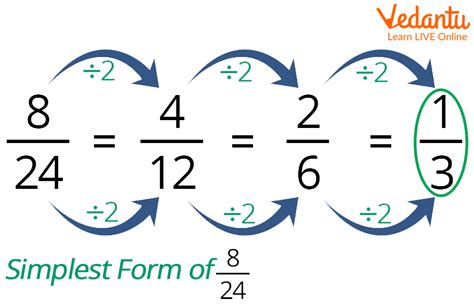
The concept of simplifying fractions is a fundamental aspect of mathematics, and it's essential to understand the process to work with fractions effectively. In this article, we'll explore the concept of simplifying fractions, specifically focusing on the fraction 12 as a fraction in its simplest form.

What is a Fraction?

A fraction is a way to express a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator tells us how many equal parts we have, and the denominator tells us how many parts the whole is divided into.

What is Simplifying Fractions?

Simplifying fractions is the process of reducing a fraction to its simplest form. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both numbers by the GCD.

Why Simplify Fractions?

Simplifying fractions is essential for several reasons:

• It makes fractions easier to work with and understand.
• It reduces errors in calculations.
• It helps to avoid confusion when comparing or adding fractions.

12 as a Fraction in Simplest Form

So, what is 12 as a fraction in its simplest form? The answer is 12/1. However, this fraction can be simplified further.

Step-by-Step Simplification

1. Find the greatest common divisor (GCD) of 12 and 1. In this case, the GCD is 1.
2. Since the GCD is 1, the fraction is already in its simplest form.

Therefore, 12 as a fraction in its simplest form is 12/1.

Real-World Applications

Simplifying fractions has numerous real-world applications, including:

• Cooking and recipes: Simplifying fractions helps to ensure accurate measurements and proportions.
• Finance: Simplifying fractions is essential for calculating interest rates, investments, and other financial transactions.
• Science and engineering: Simplifying fractions is crucial for calculating ratios, proportions, and other mathematical relationships.

Common Mistakes to Avoid

When simplifying fractions, it's essential to avoid common mistakes, such as:

• Not finding the greatest common divisor (GCD) correctly.
• Not dividing both numbers by the GCD.
• Not checking if the fraction can be simplified further.

Tips and Tricks

• Always find the greatest common divisor (GCD) of the numerator and denominator.
• Divide both numbers by the GCD to simplify the fraction.
• Check if the fraction can be simplified further by finding the GCD of the new numerator and denominator.

Conclusion

In conclusion, simplifying fractions is an essential mathematical concept that has numerous real-world applications. By understanding the process of simplifying fractions, you can work with fractions more effectively and avoid common mistakes. Remember to always find the greatest common divisor (GCD) and divide both numbers by the GCD to simplify fractions.

Now, we invite you to share your thoughts and experiences with simplifying fractions. Do you have any favorite tips or tricks for working with fractions? Share your comments below!