5 Ways To Write A Parabola Equation In Vertex Form

Quick Links :

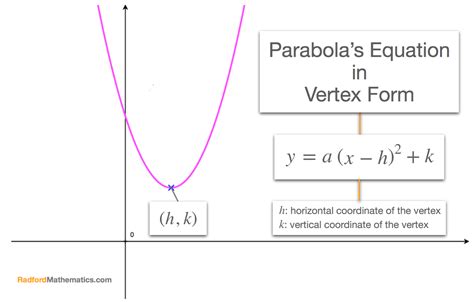
The parabola equation is a fundamental concept in algebra and geometry, and understanding how to write it in vertex form is essential for solving problems involving quadratic functions. In this article, we will explore five different methods for writing a parabola equation in vertex form, along with practical examples and explanations.

Method 1: Using the Vertex Formula

One of the simplest ways to write a parabola equation in vertex form is by using the vertex formula. The vertex formula is given by:

h = -b / 2a

where (h, k) is the vertex of the parabola, and a, b, and c are the coefficients of the quadratic equation. Once you have found the vertex, you can write the equation in vertex form as:

y = a(x - h)^2 + k

For example, let's consider the quadratic equation:

y = x^2 + 4x + 4

To write this equation in vertex form, we need to find the vertex. Using the vertex formula, we get:

h = -4 / 2(1) = -2

k = (-2)^2 + 4(-2) + 4 = 0

So, the vertex is (-2, 0), and the equation in vertex form is:

y = (x + 2)^2

Method 2: Completing the Square

Another method for writing a parabola equation in vertex form is by completing the square. This method involves manipulating the quadratic equation to create a perfect square trinomial.

For example, let's consider the quadratic equation:

y = x^2 + 6x + 8

To complete the square, we need to add and subtract (b/2)^2 to the equation:

y = x^2 + 6x + 9 - 1

y = (x + 3)^2 - 1

So, the equation in vertex form is:

y = (x + 3)^2 - 1

Method 3: Using the Factored Form

If you have a quadratic equation in factored form, you can easily write it in vertex form by using the factored form. The factored form of a quadratic equation is given by:

y = a(x - r)(x - s)

where r and s are the roots of the equation.

For example, let's consider the quadratic equation:

y = (x - 2)(x - 4)

To write this equation in vertex form, we need to expand the factored form:

y = x^2 - 6x + 8

Using the vertex formula, we get:

h = -(-6) / 2(1) = 3

k = (3)^2 - 6(3) + 8 = -1

So, the vertex is (3, -1), and the equation in vertex form is:

y = (x - 3)^2 - 1

Method 4: Using the Graphing Method

You can also write a parabola equation in vertex form by using the graphing method. This method involves graphing the quadratic equation and identifying the vertex from the graph.

For example, let's consider the quadratic equation:

y = x^2 - 2x - 3

To graph this equation, we can use a graphing calculator or a graphing software. From the graph, we can identify the vertex as (1, -4).

So, the equation in vertex form is:

y = (x - 1)^2 - 4

Method 5: Using the Standard Form

Finally, you can write a parabola equation in vertex form by using the standard form. The standard form of a quadratic equation is given by:

y = ax^2 + bx + c

To write this equation in vertex form, you can use the vertex formula to find the vertex, and then use the vertex to write the equation in vertex form.

For example, let's consider the quadratic equation:

y = 2x^2 - 4x - 6

Using the vertex formula, we get:

h = -(-4) / 2(2) = 1

k = (1)^2 - 4(1) - 6 = -9

So, the vertex is (1, -9), and the equation in vertex form is:

y = 2(x - 1)^2 - 9

In conclusion, there are several methods for writing a parabola equation in vertex form, including using the vertex formula, completing the square, using the factored form, using the graphing method, and using the standard form. Each method has its own advantages and disadvantages, and the choice of method depends on the specific problem and the level of difficulty.

We hope this article has been helpful in explaining the different methods for writing a parabola equation in vertex form. If you have any questions or need further clarification, please don't hesitate to ask.