Write The Equation In Logarithmic Form: 125=4^3

Quick Links :

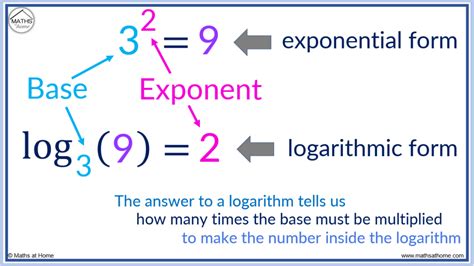
The equation can be rewritten in logarithmic form as:

3 = log4(125)

This is read as "3 is equal to the logarithm of 125 with a base of 4".

Here's a brief explanation of how we got there:

• The original equation is 125 = 4^3, which means that 125 is equal to 4 raised to the power of 3.
• In logarithmic form, we want to represent the exponent (3) as the result of a logarithm.
• The base of the logarithm is 4, because that's the base of the original exponential expression.
• The argument of the logarithm (the value inside the parentheses) is 125, because that's the result of the original exponential expression.

So, the logarithmic form of the equation is 3 = log4(125).

What is Logarithmic Form?

Logarithmic form is a way of expressing an exponential equation as a logarithmic equation. It's a fundamental concept in mathematics, and it has many practical applications in science, engineering, and finance.

In general, a logarithmic equation has the form:

y = logb(x)

Where:

• y is the exponent
• b is the base
• x is the argument (the value inside the parentheses)

The logarithmic form is useful because it allows us to work with very large or very small numbers in a more manageable way. It's also a key tool in many mathematical and scientific applications, such as solving equations, finding roots, and modeling real-world phenomena.

How to Convert Exponential Form to Logarithmic Form

Converting an exponential equation to logarithmic form is a straightforward process. Here are the steps:

1. Identify the base and the exponent in the exponential equation.
2. Identify the result of the exponential equation (the value that the exponent is being raised to).
3. Write the logarithmic equation in the form y = logb(x), where:
   • y is the exponent
   • b is the base
   • x is the result of the exponential equation

For example, let's convert the exponential equation 2^5 = 32 to logarithmic form.

• The base is 2, and the exponent is 5.
• The result of the exponential equation is 32.
• So, the logarithmic form is: 5 = log2(32)

Note that the logarithmic form is a more compact and elegant way of expressing the equation, and it's often easier to work with than the exponential form.

Key Concepts and Vocabulary

• Exponential equation: An equation in which a base is raised to a power, such as 2^3 = 8.
• Logarithmic equation: An equation in which the exponent is the result of a logarithm, such as 3 = log2(8).
• Base: The number that is being raised to a power in an exponential equation.
• Exponent: The power to which the base is being raised in an exponential equation.
• Argument: The value inside the parentheses in a logarithmic equation.
• Logarithm: A mathematical operation that finds the exponent to which a base must be raised to produce a given value.

By understanding the concepts and vocabulary of logarithmic form, you'll be able to work with logarithmic equations and apply them to a wide range of problems and applications.

Common Applications of Logarithmic Form

Logarithmic form has many practical applications in science, engineering, and finance. Here are a few examples:

• Science: Logarithmic form is used to model population growth, chemical reactions, and other real-world phenomena.
• Engineering: Logarithmic form is used to design electronic circuits, calculate stresses and strains, and optimize system performance.
• Finance: Logarithmic form is used to calculate interest rates, investment returns, and other financial metrics.

In general, logarithmic form is a powerful tool for working with very large or very small numbers, and it's an essential concept in many mathematical and scientific applications.

Conclusion

In conclusion, logarithmic form is a fundamental concept in mathematics that allows us to express exponential equations in a more compact and elegant way. By understanding the concepts and vocabulary of logarithmic form, you'll be able to work with logarithmic equations and apply them to a wide range of problems and applications. Whether you're a student, scientist, or engineer, logarithmic form is an essential tool to have in your mathematical toolkit.

FAQ Section: