Write Quadratic Equation In Standard Form Easily

Quick Links :

Quadratic equations are a fundamental concept in algebra, and understanding how to write them in standard form is essential for solving and analyzing these equations. In this article, we'll explore the concept of quadratic equations, the importance of standard form, and provide a step-by-step guide on how to write quadratic equations in standard form easily.

What is a Quadratic Equation?

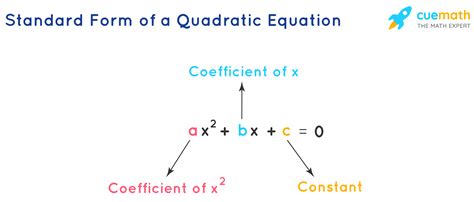
A quadratic equation is a polynomial equation of degree two, which means the highest power of the variable (usually x) is two. It has the general form of ax^2 + bx + c = 0, where a, b, and c are constants, and x is the variable. Quadratic equations can be used to model real-world problems, such as the trajectory of a projectile, the shape of a mirror, or the growth of a population.

Why is Standard Form Important?

Standard form is essential in quadratic equations because it allows us to easily identify the coefficients (a, b, and c) and the roots of the equation. The standard form of a quadratic equation is ax^2 + bx + c = 0, where a, b, and c are constants, and x is the variable. By writing a quadratic equation in standard form, we can apply various techniques to solve it, such as factoring, quadratic formula, or graphing.

Step-by-Step Guide to Writing Quadratic Equations in Standard Form

To write a quadratic equation in standard form, follow these steps:

1. Identify the coefficients: Identify the coefficients a, b, and c in the given equation.
2. Rearrange the terms: Rearrange the terms in the equation to match the standard form ax^2 + bx + c = 0.
3. Simplify the equation: Simplify the equation by combining like terms and eliminating any unnecessary parentheses.

Here's an example:

Suppose we have the equation x^2 + 5x - 6 = 0. To write it in standard form, we need to identify the coefficients:

• a = 1
• b = 5
• c = -6

The equation is already in standard form, so no rearrangement is needed.

Another example:

Suppose we have the equation 2x^2 - 3x - 4 = 2x^2 + 2x - 5. To write it in standard form, we need to:

• Identify the coefficients: a = 2, b = -3, and c = -4
• Rearrange the terms: 2x^2 - 3x - 4 - 2x^2 - 2x + 5 = 0
• Simplify the equation: -5x + 1 = 0

This equation is not in standard form yet. To fix this, we need to move the constant term to the right-hand side:

-5x = -1

Now, we can write the equation in standard form:

5x - 1 = 0

Common Pitfalls and Solutions

When writing quadratic equations in standard form, there are some common pitfalls to avoid:

• Incorrect coefficient values: Double-check the coefficients a, b, and c to ensure they are accurate.
• Incorrect rearrangement: Make sure to rearrange the terms correctly to match the standard form.
• Simplification errors: Simplify the equation carefully to avoid eliminating or adding unnecessary terms.

To avoid these pitfalls, it's essential to:

• Take your time and work slowly
• Double-check your calculations
• Use visual aids, such as graphs or charts, to help identify errors

Real-World Applications of Quadratic Equations

Quadratic equations have numerous real-world applications, including:

• Physics and Engineering: Quadratic equations are used to model the trajectory of projectiles, the shape of mirrors, and the growth of populations.
• Economics: Quadratic equations are used to model supply and demand curves, and to determine the optimal price for a product.
• Computer Science: Quadratic equations are used in computer graphics, game development, and algorithm design.

Conclusion

Writing quadratic equations in standard form is a crucial skill in algebra and has numerous real-world applications. By following the steps outlined in this article, you can easily write quadratic equations in standard form and solve them using various techniques. Remember to avoid common pitfalls, take your time, and double-check your calculations to ensure accuracy.

Do you have any questions about writing quadratic equations in standard form? Share your thoughts and feedback in the comments below!