Simplifying radical expressions is an essential skill in mathematics, particularly in algebra and geometry. Radical expressions are mathematical expressions that contain radicals, which are symbols used to indicate the root of a number. Simplifying these expressions helps to make them easier to work with and understand. In this article, we will explore five ways to simplify radical expressions, along with examples and explanations to help you master this skill.
Understanding Radical Expressions

Before we dive into simplifying radical expressions, it's essential to understand what they are and how they work. A radical expression is a mathematical expression that contains a radical, which is a symbol used to indicate the root of a number. For example, the expression √(x+3) is a radical expression because it contains the radical symbol √. Radical expressions can be used to represent a wide range of mathematical concepts, including square roots, cube roots, and nth roots.
Method 1: Factoring Out Perfect Squares

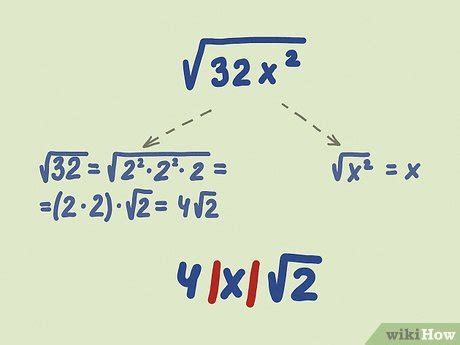
One way to simplify radical expressions is to factor out perfect squares. A perfect square is a number that can be expressed as the square of an integer. For example, 16 is a perfect square because it can be expressed as 4^2. When simplifying radical expressions, look for perfect squares that can be factored out of the expression. This can help to simplify the expression and make it easier to work with.
For example, consider the expression √(16x+16). This expression can be simplified by factoring out the perfect square 16:
√(16x+16) = √(16(x+1)) = 4√(x+1)
Method 2: Factoring Out Perfect Cubes

Another way to simplify radical expressions is to factor out perfect cubes. A perfect cube is a number that can be expressed as the cube of an integer. For example, 27 is a perfect cube because it can be expressed as 3^3. When simplifying radical expressions, look for perfect cubes that can be factored out of the expression. This can help to simplify the expression and make it easier to work with.
For example, consider the expression ∛(27x+27). This expression can be simplified by factoring out the perfect cube 27:
∛(27x+27) = ∛(27(x+1)) = 3∛(x+1)
Method 3: Simplifying Radicals with Variables

Radical expressions can also be simplified by simplifying radicals with variables. When simplifying radicals with variables, look for any common factors that can be factored out of the expression. This can help to simplify the expression and make it easier to work with.
For example, consider the expression √(x^2+2x+1). This expression can be simplified by factoring out the common factor (x+1):
√(x^2+2x+1) = √((x+1)^2) = x+1
Method 4: Rationalizing the Denominator

Another way to simplify radical expressions is to rationalize the denominator. Rationalizing the denominator involves eliminating any radicals in the denominator of the expression. This can be done by multiplying the numerator and denominator by a clever form of 1, which will eliminate the radical in the denominator.
For example, consider the expression 1/√2. This expression can be simplified by rationalizing the denominator:
1/√2 = 1/√2 * (√2/√2) = √2/2
Method 5: Simplifying Complex Radicals

Finally, radical expressions can also be simplified by simplifying complex radicals. Complex radicals are radical expressions that contain multiple radicals or radical expressions with variables. When simplifying complex radicals, look for any common factors that can be factored out of the expression. This can help to simplify the expression and make it easier to work with.
For example, consider the expression √(x+√(x^2+1)). This expression can be simplified by factoring out the common factor (x+1):
√(x+√(x^2+1)) = √((x+1)^2) = x+1
In conclusion, simplifying radical expressions is an essential skill in mathematics that can be achieved through several methods. By factoring out perfect squares, perfect cubes, and simplifying radicals with variables, rationalizing the denominator, and simplifying complex radicals, you can simplify even the most complex radical expressions. With practice and patience, you can master these skills and become proficient in simplifying radical expressions.
What is a radical expression?
+A radical expression is a mathematical expression that contains a radical, which is a symbol used to indicate the root of a number.
How do I simplify a radical expression?
+There are several ways to simplify radical expressions, including factoring out perfect squares, perfect cubes, and simplifying radicals with variables, rationalizing the denominator, and simplifying complex radicals.
What is a perfect square?
+A perfect square is a number that can be expressed as the square of an integer. For example, 16 is a perfect square because it can be expressed as 4^2.