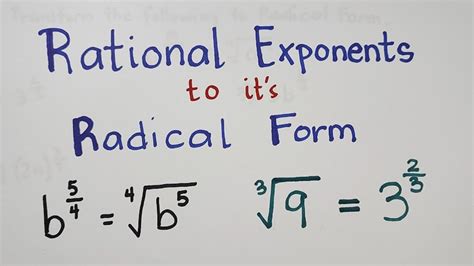Converting Expressions To Radical Form Made Easy

Quick Links :

Simplifying radical expressions is a fundamental concept in mathematics, particularly in algebra and geometry. Radical expressions are mathematical expressions that contain a radical sign, such as √, ∛, or ∜. Understanding how to convert expressions to radical form is crucial for solving various types of equations and problems. In this article, we will explore the step-by-step process of converting expressions to radical form, along with practical examples and tips.

What is Radical Form?

A radical expression is in radical form when it is written with a radical sign and the radicand (the number or expression inside the radical sign) is simplified as much as possible. The radical sign indicates that we need to find the root of the radicand. For instance, the square root of a number x can be written as √x.

Why is Converting to Radical Form Important?

Converting expressions to radical form is essential for several reasons:

• Simplifies complex expressions: Radical form makes it easier to simplify complex expressions and equations.
• Facilitates calculations: Radical form can simplify calculations by allowing us to manipulate the expression more easily.
• Solves equations: Converting expressions to radical form is necessary for solving certain types of equations, such as quadratic equations.

Step-by-Step Guide to Converting Expressions to Radical Form

Converting expressions to radical form involves several steps:

1. Factor the radicand: Factor the radicand into its prime factors.
2. Identify perfect squares or cubes: Identify any perfect squares or cubes within the radicand.
3. Simplify the radicand: Simplify the radicand by combining like terms and canceling out any common factors.
4. Write the expression in radical form: Write the expression in radical form, using the simplified radicand and the correct radical sign.

Examples of Converting Expressions to Radical Form

Let's consider a few examples:

• Convert the expression √(x^2 + 4) to radical form.
  • Factor the radicand: x^2 + 4 = (x + 2)(x - 2)
  • Identify perfect squares or cubes: None
  • Simplify the radicand: (x + 2)(x - 2) = x^2 - 4
  • Write the expression in radical form: √(x^2 - 4)
• Convert the expression ∛(27x^3) to radical form.
  • Factor the radicand: 27x^3 = 3^3 x^3
  • Identify perfect squares or cubes: 3^3 is a perfect cube
  • Simplify the radicand: 3^3 x^3 = (3x)^3
  • Write the expression in radical form: ∛(3x)^3 = 3x

Tips and Tricks for Converting Expressions to Radical Form

Here are some tips and tricks to keep in mind when converting expressions to radical form:

• Always factor the radicand before simplifying.
• Identify perfect squares or cubes to simplify the radicand.
• Cancel out any common factors between the radicand and the radical sign.
• Use the correct radical sign (√, ∛, or ∜) depending on the type of root.

Common Mistakes to Avoid When Converting Expressions to Radical Form

When converting expressions to radical form, avoid the following common mistakes:

• Forgetting to factor the radicand
• Not identifying perfect squares or cubes
• Not simplifying the radicand correctly
• Using the wrong radical sign

Conclusion

Converting expressions to radical form is an essential skill in mathematics, particularly in algebra and geometry. By following the step-by-step guide and tips outlined in this article, you can simplify complex expressions and solve various types of equations. Remember to factor the radicand, identify perfect squares or cubes, and simplify the radicand correctly. With practice and patience, you will become proficient in converting expressions to radical form.

Now, it's your turn to try! Take a few minutes to practice converting expressions to radical form using the steps and tips outlined in this article. Share your thoughts and questions in the comments below.