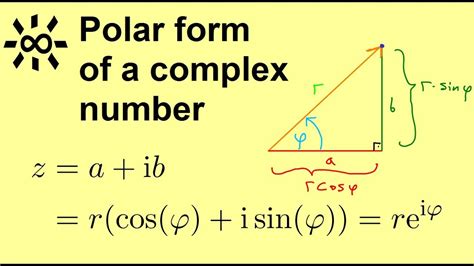Convert Complex Numbers To Polar Form In 3 Easy Steps

Quick Links :

Complex numbers are a fundamental concept in mathematics and engineering, and converting them to polar form is a crucial skill. In this article, we will explore the importance of converting complex numbers to polar form and provide a step-by-step guide on how to do it in 3 easy steps.

Complex numbers have both real and imaginary components, and they can be represented in the form a + bi, where a is the real part and b is the imaginary part. However, in many applications, it is more convenient to represent complex numbers in polar form, which consists of a magnitude (or length) and an angle.

Why Convert Complex Numbers to Polar Form?

Converting complex numbers to polar form has several advantages. One of the main reasons is that it simplifies many mathematical operations, such as multiplication and division. In polar form, these operations become much easier to perform, and the results are often more intuitive. Additionally, polar form is often more convenient for representing complex numbers in graphical form, such as in the complex plane.

Step 1: Calculate the Magnitude

The first step in converting a complex number to polar form is to calculate the magnitude, also known as the length or modulus. The magnitude is calculated using the formula:

r = √(a^2 + b^2)

where a is the real part and b is the imaginary part of the complex number.

For example, let's consider the complex number 3 + 4i. To calculate the magnitude, we would use the formula:

r = √(3^2 + 4^2) = √(9 + 16) = √25 = 5

Step 2: Calculate the Angle

The second step is to calculate the angle, also known as the argument or phase angle. The angle is calculated using the formula:

θ = arctan(b/a)

where a is the real part and b is the imaginary part of the complex number.

Using the same example as before, we would calculate the angle as follows:

θ = arctan(4/3) = arctan(1.33) ≈ 53.13°

Step 3: Write the Complex Number in Polar Form

The final step is to write the complex number in polar form using the calculated magnitude and angle. The polar form is written as:

z = r(cos(θ) + i sin(θ))

where r is the magnitude and θ is the angle.

Using the calculated values from before, we would write the complex number 3 + 4i in polar form as:

z = 5(cos(53.13°) + i sin(53.13°))

Benefits of Converting Complex Numbers to Polar Form

Converting complex numbers to polar form has several benefits, including:

• Simplified mathematical operations: Polar form makes it easier to perform operations such as multiplication and division.
• Improved graphical representation: Polar form is often more convenient for representing complex numbers in graphical form.
• Increased accuracy: Polar form can provide more accurate results in certain applications.

Common Applications of Polar Form

Polar form has many applications in mathematics, engineering, and physics, including:

• Signal processing: Polar form is often used in signal processing to represent complex signals.
• Control systems: Polar form is used in control systems to analyze and design control systems.
• Navigation: Polar form is used in navigation systems to represent complex navigation data.

Conclusion

In conclusion, converting complex numbers to polar form is a crucial skill in mathematics and engineering. By following the 3 easy steps outlined in this article, you can convert complex numbers to polar form and take advantage of the many benefits it has to offer. Whether you're working on a complex engineering project or simply need to represent complex numbers in a more intuitive way, polar form is an essential tool to have in your mathematical toolkit.

We hope this article has been informative and helpful in your understanding of complex numbers and polar form. If you have any questions or comments, please feel free to share them below.