Angles That Form A Triangle

Quick Links :

Triangles are a fundamental concept in geometry, and understanding the angles that form a triangle is crucial for various mathematical and real-world applications. The angles of a triangle are the building blocks of the shape, and they play a significant role in determining the properties and behavior of the triangle.

The study of triangles and their angles has numerous practical applications in fields such as architecture, engineering, physics, and computer science. From designing bridges and buildings to calculating distances and velocities, triangles are an essential part of problem-solving in these fields. Moreover, the angles of a triangle are a critical aspect of trigonometry, which is a branch of mathematics that deals with the relationships between the sides and angles of triangles.

Understanding the Basics of Triangle Angles

In a triangle, there are three angles, and the sum of these angles is always 180 degrees. This is known as the angle sum property of triangles. Each angle of a triangle is measured in degrees, and it is usually denoted by a symbol such as ∠A, ∠B, or ∠C.

There are several types of angles in a triangle, including acute, right, obtuse, and straight angles. An acute angle is less than 90 degrees, while a right angle is exactly 90 degrees. An obtuse angle is greater than 90 degrees but less than 180 degrees, and a straight angle is equal to 180 degrees.

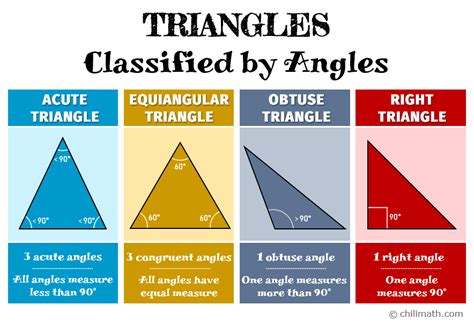
Types of Triangles Based on Angles

Triangles can be classified based on their angles, and there are several types of triangles, including:

• Acute Triangle: A triangle with all acute angles is called an acute triangle.
• Right Triangle: A triangle with one right angle is called a right triangle.
• Obtuse Triangle: A triangle with one obtuse angle is called an obtuse triangle.
• Equiangular Triangle: A triangle with all equal angles is called an equiangular triangle.

Properties of Triangle Angles

Triangle angles have several important properties, including:

• Angle Sum Property: The sum of the angles of a triangle is always 180 degrees.
• Exterior Angle Property: The exterior angle of a triangle is equal to the sum of the remote interior angles.
• Alternate Interior Angle Property: If two lines intersect a triangle, then the alternate interior angles are congruent.
• Corresponding Angle Property: If two lines intersect a triangle, then the corresponding angles are congruent.

Real-World Applications of Triangle Angles

Triangle angles have numerous real-world applications in various fields, including:

• Architecture: Triangle angles are used in the design of buildings, bridges, and other structures to ensure stability and balance.
• Engineering: Triangle angles are used in the design of electronic circuits, mechanical systems, and other devices.
• Physics: Triangle angles are used to calculate distances, velocities, and forces in various physical systems.
• Computer Science: Triangle angles are used in computer graphics, game development, and other applications.

Calculating Triangle Angles

There are several formulas and techniques for calculating triangle angles, including:

• Law of Cosines: This formula relates the lengths of the sides of a triangle to the cosine of one of its angles.
• Law of Sines: This formula relates the lengths of the sides of a triangle to the sine of one of its angles.
• Angle Bisector Theorem: This theorem relates the lengths of the sides of a triangle to the angle bisector.

Practical Examples of Calculating Triangle Angles

Here are some practical examples of calculating triangle angles:

• Example 1: Calculate the angles of a triangle with sides of length 3, 4, and 5.
• Example 2: Calculate the angles of a triangle with sides of length 5, 12, and 13.
• Example 3: Calculate the angles of a triangle with sides of length 7, 24, and 25.

In conclusion, the angles of a triangle are a fundamental concept in geometry, and understanding them is crucial for various mathematical and real-world applications. By understanding the properties and formulas related to triangle angles, we can solve problems and calculate distances, velocities, and forces in various fields.

We hope this article has provided you with a comprehensive understanding of the angles that form a triangle. If you have any questions or comments, please feel free to share them below.