5 Ways To Write Expressions In Radical Form

Quick Links :

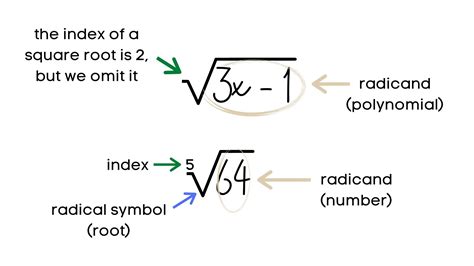
Mathematics is a language that describes the world around us, and mastering its nuances can unlock a deeper understanding of the universe. One of the fundamental concepts in mathematics is the use of radicals to express complex numbers and quantities. In this article, we will delve into the world of radical expressions and explore five ways to write them.

Radical expressions are used to represent numbers that cannot be expressed as simple fractions or whole numbers. They involve the use of roots, such as square roots, cube roots, and higher-order roots, to simplify complex expressions. Radical expressions are essential in various mathematical operations, including algebra, geometry, and calculus.

1. Simplifying Radical Expressions

One of the primary ways to write radical expressions is by simplifying them. This involves factoring out perfect squares or perfect cubes from the radicand (the number inside the radical). For example, the expression √(4x^2) can be simplified as 2x, since the square root of 4 is 2.

Here are some steps to simplify radical expressions:

• Factor the radicand into its prime factors.
• Identify perfect squares or perfect cubes.
• Simplify the expression by factoring out the perfect squares or perfect cubes.

Example:

Simplify the expression √(9x^4).

• Factor the radicand: 9x^4 = 3^2 × x^4
• Identify perfect squares: 3^2 and x^4 can be written as (x^2)^2
• Simplify the expression: √(9x^4) = 3x^2

2. Rationalizing the Denominator

Another way to write radical expressions is by rationalizing the denominator. This involves multiplying the numerator and denominator by a radical expression that eliminates the radical from the denominator.

Here are some steps to rationalize the denominator:

• Identify the radical expression in the denominator.
• Multiply the numerator and denominator by a radical expression that eliminates the radical.
• Simplify the expression.

Example:

Rationalize the denominator of the expression 1/√2.

• Multiply the numerator and denominator by √2: (1/√2) × (√2/√2) = √2/2

3. Adding and Subtracting Radical Expressions

Radical expressions can be added and subtracted in a similar way to algebraic expressions. However, the radicals must be like terms, meaning they have the same radicand and index.

Here are some steps to add and subtract radical expressions:

• Identify like terms.
• Combine the like terms.
• Simplify the expression.

Example:

Add the expressions 2√3 + 3√3.

• Identify like terms: 2√3 and 3√3 have the same radicand and index.
• Combine the like terms: 2√3 + 3√3 = 5√3

4. Multiplying Radical Expressions

Radical expressions can be multiplied by multiplying the radicands and adding the indices. This rule applies to both square roots and higher-order roots.

Here are some steps to multiply radical expressions:

• Multiply the radicands.
• Add the indices.
• Simplify the expression.

Example:

Multiply the expressions √2 × √3.

• Multiply the radicands: 2 × 3 = 6
• Add the indices: √6

5. Dividing Radical Expressions

Radical expressions can be divided by dividing the radicands and subtracting the indices. This rule applies to both square roots and higher-order roots.

Here are some steps to divide radical expressions:

• Divide the radicands.
• Subtract the indices.
• Simplify the expression.

Example:

Divide the expressions √6 ÷ √2.

• Divide the radicands: 6 ÷ 2 = 3
• Subtract the indices: √3

In conclusion, mastering the art of writing radical expressions is crucial in mathematics. By simplifying, rationalizing, adding, subtracting, multiplying, and dividing radical expressions, we can unlock a deeper understanding of mathematical concepts. We hope this article has provided you with a comprehensive guide to writing radical expressions. Share your thoughts and questions in the comments below!