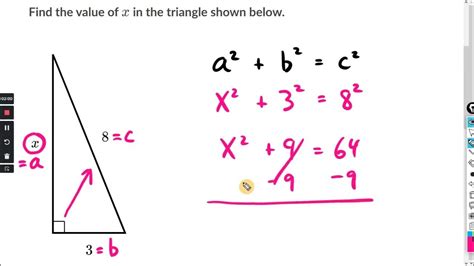Right triangles are a fundamental concept in geometry and trigonometry, and identifying their side lengths is crucial for solving various problems. In this article, we will explore three ways to identify right triangle side lengths, including the Pythagorean theorem, trigonometric ratios, and the properties of special right triangles.
Understanding Right Triangles

A right triangle is a triangle with one right angle (90 degrees). The side opposite the right angle is called the hypotenuse, and the other two sides are called legs. The lengths of the legs and hypotenuse are related in a specific way, which is the key to identifying their lengths.
Method 1: The Pythagorean Theorem

The Pythagorean theorem states that the square of the length of the hypotenuse (c) is equal to the sum of the squares of the lengths of the legs (a and b). Mathematically, this can be expressed as:
a^2 + b^2 = c^2
This theorem can be used to find the length of the hypotenuse or one of the legs, given the lengths of the other two sides. For example, if the lengths of the legs are 3 and 4, the length of the hypotenuse can be calculated as:
c^2 = 3^2 + 4^2 c^2 = 9 + 16 c^2 = 25 c = √25 c = 5
Example Problems
- Find the length of the hypotenuse of a right triangle with legs of length 5 and 12.
- Find the length of one leg of a right triangle with a hypotenuse of length 10 and the other leg of length 6.
Method 2: Trigonometric Ratios

Trigonometric ratios are relationships between the lengths of the sides of a right triangle and the angles. The three most common trigonometric ratios are sine, cosine, and tangent. These ratios can be used to find the length of a side or an angle, given the lengths of the other two sides and one angle.
- Sine (sin): opposite side / hypotenuse
- Cosine (cos): adjacent side / hypotenuse
- Tangent (tan): opposite side / adjacent side
For example, if the length of the hypotenuse is 10 and the angle opposite one leg is 30 degrees, the length of that leg can be calculated as:
sin(30) = opposite side / 10 0.5 = opposite side / 10 opposite side = 5
Example Problems
- Find the length of one leg of a right triangle with a hypotenuse of length 15 and an angle of 45 degrees.
- Find the length of the hypotenuse of a right triangle with one leg of length 8 and an angle of 60 degrees.
Method 3: Special Right Triangles

Special right triangles are triangles with specific angle measures that make it easy to identify their side lengths. The most common special right triangles are the 30-60-90 triangle and the 45-45-90 triangle.
- 30-60-90 triangle: The side lengths are in the ratio 1:√3:2.
- 45-45-90 triangle: The side lengths are in the ratio 1:1:√2.
For example, if a right triangle has angles of 30, 60, and 90 degrees, and the length of the shorter leg is 3, the length of the hypotenuse can be calculated as:
hypotenuse = 2 × shorter leg hypotenuse = 2 × 3 hypotenuse = 6
Example Problems
- Find the length of the hypotenuse of a 30-60-90 triangle with a shorter leg of length 5.
- Find the length of one leg of a 45-45-90 triangle with a hypotenuse of length 10.
We hope this article has helped you understand the different ways to identify right triangle side lengths. Whether you use the Pythagorean theorem, trigonometric ratios, or the properties of special right triangles, being able to identify these side lengths is essential for solving various problems in geometry and trigonometry.
We invite you to share your thoughts and questions in the comments section below. What methods do you find most helpful for identifying right triangle side lengths? Do you have any favorite example problems or real-world applications? Share your insights and let's continue the conversation!
What is the Pythagorean theorem?
+The Pythagorean theorem states that the square of the length of the hypotenuse (c) is equal to the sum of the squares of the lengths of the legs (a and b): a^2 + b^2 = c^2.
What are trigonometric ratios?
+Trigonometric ratios are relationships between the lengths of the sides of a right triangle and the angles. The three most common trigonometric ratios are sine, cosine, and tangent.
What are special right triangles?
+Special right triangles are triangles with specific angle measures that make it easy to identify their side lengths. The most common special right triangles are the 30-60-90 triangle and the 45-45-90 triangle.