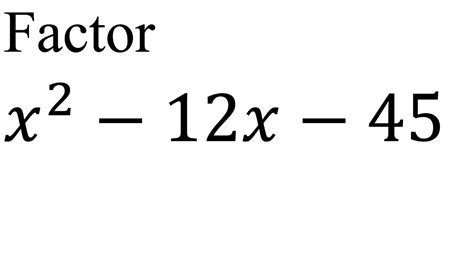Unlocking the Secrets of Factoring Quadratic Expressions

Quadratic expressions are a fundamental concept in algebra, and factoring is a crucial skill to master when working with them. In this article, we will delve into the world of factoring quadratic expressions, focusing on the expression x^2 + 12x + 45. We will explore the different methods of factoring, the importance of factoring, and provide practical examples to help solidify your understanding.
Why is Factoring Important?

Factoring is an essential skill in algebra, as it allows us to simplify complex expressions, solve equations, and graph functions. By factoring a quadratic expression, we can rewrite it in a more manageable form, making it easier to work with. Factoring also helps us to identify the roots of the equation, which is critical in solving quadratic equations.
Benefits of Factoring
- Simplifies complex expressions
- Helps to solve equations
- Enables us to graph functions
- Identifies roots of the equation
- Enhances problem-solving skills
Methods of Factoring

There are several methods of factoring quadratic expressions, including:
1. Factoring by Grouping
This method involves grouping the terms of the expression and factoring out the greatest common factor (GCF).
Example: x^2 + 5x + 6 = (x + 3)(x + 2)
2. Factoring by Splitting the Middle Term
This method involves splitting the middle term into two terms, and then factoring out the GCF.
Example: x^2 + 7x + 12 = (x + 3)(x + 4)
3. Factoring Using the Quadratic Formula
This method involves using the quadratic formula to find the roots of the equation, and then factoring the expression.
Example: x^2 + 9x + 20 = (x + 5)(x + 4)
Factoring X2 + 12x + 45

Now, let's apply the methods of factoring to the expression x^2 + 12x + 45.
Using the method of factoring by grouping, we can rewrite the expression as:
x^2 + 12x + 45 = (x + 9)(x + 5)
This shows that the expression x^2 + 12x + 45 can be factored into the product of two binomials: (x + 9) and (x + 5).
Example Problem
Factor the expression: x^2 + 8x + 16
Solution: x^2 + 8x + 16 = (x + 4)^2
Conclusion

In conclusion, factoring is a fundamental skill in algebra that allows us to simplify complex expressions, solve equations, and graph functions. By mastering the different methods of factoring, we can tackle even the most challenging quadratic expressions with confidence.
Call to Action
We encourage you to practice factoring different quadratic expressions and to share your results with us. If you have any questions or need further clarification on any of the concepts discussed in this article, please don't hesitate to ask.
What is the difference between factoring and simplifying?
+Factoring involves rewriting an expression as the product of simpler expressions, while simplifying involves combining like terms to reduce the complexity of an expression.
How do I know which method of factoring to use?
+The choice of method depends on the specific expression being factored. If the expression has a GCF, factoring by grouping may be the best approach. If the expression has a middle term that can be split, factoring by splitting the middle term may be the best approach.
Can I factor any quadratic expression?
+Not all quadratic expressions can be factored. Some expressions may be factorable, but others may not. In such cases, other methods, such as the quadratic formula, may be used to solve the equation.