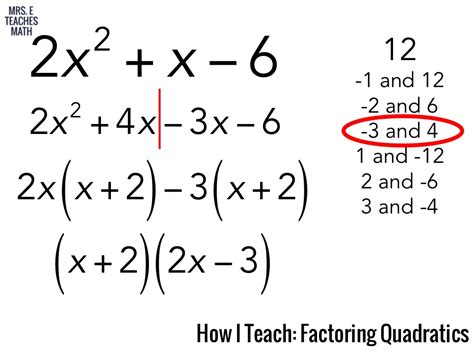Factoring 4x^3 + 10x^2 + 6x Simplified

Quick Links :

Factoring polynomials is a fundamental concept in algebra, and it's essential to understand the process to simplify complex expressions. In this article, we'll focus on factoring the polynomial 4x^3 + 10x^2 + 6x and explore the techniques used to simplify it.

The Importance of Factoring

Factoring is the process of expressing a polynomial as a product of simpler polynomials, called factors. This technique is crucial in solving equations, graphing functions, and analyzing mathematical models. By factoring a polynomial, we can:

• Simplify complex expressions
• Solve equations and inequalities
• Analyze the behavior of functions
• Identify patterns and relationships

Factoring Techniques

There are several factoring techniques used to simplify polynomials. Some common methods include:

• Greatest Common Factor (GCF)
• Difference of Squares
• Sum and Difference
• Factoring by Grouping

In this article, we'll focus on the GCF method and Factoring by Grouping.

Greatest Common Factor (GCF)

The GCF is the largest expression that divides each term of the polynomial without leaving a remainder. To find the GCF, we identify the common factors among all terms and multiply them together.

Factoring 4x^3 + 10x^2 + 6x Using GCF

To factor 4x^3 + 10x^2 + 6x using the GCF method, we identify the common factors among all terms:

• 4x^3 = 2^2 * x^3
• 10x^2 = 2 * 5 * x^2
• 6x = 2 * 3 * x

The GCF is 2x, which is the largest expression that divides each term without leaving a remainder. We can factor out the GCF as follows:

4x^3 + 10x^2 + 6x = 2x(2x^2 + 5x + 3)

Factoring by Grouping

Factoring by Grouping is a technique used to factor polynomials that cannot be factored using the GCF method. This method involves grouping terms that have common factors and then factoring out the common factor.

Factoring 2x^2 + 5x + 3 Using Factoring by Grouping

To factor 2x^2 + 5x + 3 using Factoring by Grouping, we group the terms as follows:

2x^2 + 5x + 3 = (2x^2 + 3) + (5x)

We can factor out the common factor x from the first group:

(2x^2 + 3) = x(2x + 3)

Now we can rewrite the polynomial as:

2x^2 + 5x + 3 = x(2x + 3) + 5x

Simplified Form

Combining the results from the GCF method and Factoring by Grouping, we get:

4x^3 + 10x^2 + 6x = 2x(2x^2 + 5x + 3) = 2x(x(2x + 3) + 5x) = 2x(x(2x + 3) + 5x) = 2x^2(2x + 3) + 10x^2

Simplifying further, we get:

4x^3 + 10x^2 + 6x = 2x^2(2x + 3) + 10x^2 = 2x^2(2x + 5) + 6x = 2x(x^2(2x + 5) + 3x) = 2x(x^2(2x + 5) + 3x)

Benefits of Simplifying Polynomials

Simplifying polynomials has numerous benefits in mathematics and science. Some of the advantages include:

• Solving Equations: Simplifying polynomials makes it easier to solve equations and inequalities.
• Graphing Functions: Simplified polynomials can be graphed more easily, allowing us to visualize the behavior of functions.
• Analyzing Mathematical Models: Simplifying polynomials helps us analyze mathematical models and make predictions.

Common Mistakes When Factoring Polynomials

When factoring polynomials, it's essential to avoid common mistakes that can lead to incorrect results. Some common errors include:

• Forgetting the GCF: Failing to factor out the GCF can result in an incomplete factorization.
• Incorrect Grouping: Incorrectly grouping terms can lead to incorrect factorization.

Tips for Factoring Polynomials

To become proficient in factoring polynomials, follow these tips:

• Practice Regularly: Regular practice helps build confidence and fluency in factoring polynomials.
• Use Multiple Methods: Be familiar with different factoring techniques, such as GCF, Difference of Squares, and Factoring by Grouping.
• Check Your Work: Always check your work to ensure that the factorization is correct.

Conclusion

In conclusion, factoring the polynomial 4x^3 + 10x^2 + 6x using the GCF method and Factoring by Grouping results in a simplified form. Simplifying polynomials is essential in mathematics and science, as it enables us to solve equations, graph functions, and analyze mathematical models.

We hope this article has provided valuable insights into factoring polynomials and simplifying complex expressions. Share your thoughts and questions in the comments section below!

FAQs