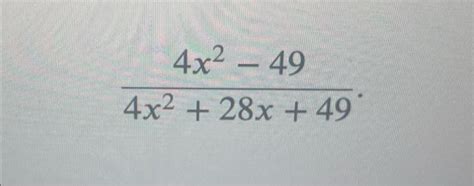Understanding the Importance of Factoring in Algebra

Factoring is a crucial concept in algebra that helps simplify complex expressions and solve equations. It involves expressing an algebraic expression as a product of its prime factors, which can be simpler polynomials or even constants. Factoring enables us to identify common factors, reduce expressions to their simplest forms, and solve equations more efficiently.
Why Factoring is Essential in Algebra
Factoring is essential in algebra because it allows us to:
- Simplify complex expressions: By factoring out common factors, we can simplify complex expressions and make them easier to work with.
- Solve equations: Factoring is a crucial step in solving quadratic equations and other types of equations.
- Identify relationships: Factoring helps us identify relationships between different variables and constants in an equation.
Factoring Quadratic Expressions

Quadratic expressions are a common type of expression that can be factored. A quadratic expression has the form ax^2 + bx + c, where a, b, and c are constants. Factoring quadratic expressions involves expressing them as a product of two binomials.
Steps to Factor a Quadratic Expression
To factor a quadratic expression, follow these steps:
- Check if the expression can be factored: Not all quadratic expressions can be factored. Check if the expression has a common factor.
- Look for two numbers whose product is ac and whose sum is b: These numbers will be used to create the two binomials.
- Write the expression as a product of two binomials: Use the numbers found in step 2 to create the two binomials.
Factoring 4x2 + 28x + 49: A Step-by-Step Guide

Now, let's apply the steps to factor the expression 4x2 + 28x + 49.
Step 1: Check if the Expression Can Be Factored
The expression 4x2 + 28x + 49 can be factored because it has a common factor.
Step 2: Look for Two Numbers Whose Product is ac and Whose Sum is b
In this case, a = 4, b = 28, and c = 49. We need to find two numbers whose product is 4 * 49 = 196 and whose sum is 28.
These numbers are 14 and 14, since 14 * 14 = 196 and 14 + 14 = 28.
Step 3: Write the Expression as a Product of Two Binomials
Using the numbers found in step 2, we can write the expression as:
4x2 + 28x + 49 = (2x + 7)(2x + 7)
Simplified Expression

The simplified expression is (2x + 7)(2x + 7) or (2x + 7)^2.
Benefits of Simplifying Expressions

Simplifying expressions has several benefits, including:
- Making complex expressions easier to work with
- Reducing errors by minimizing the number of steps required to solve an equation
- Enabling us to identify relationships between different variables and constants
Common Applications of Factoring

Factoring has numerous applications in various fields, including:
- Algebra: Factoring is used to solve equations and simplify expressions.
- Geometry: Factoring is used to find the area and perimeter of triangles and other shapes.
- Physics: Factoring is used to describe the motion of objects and solve problems involving energy and momentum.
Conclusion
In conclusion, factoring is a powerful tool in algebra that enables us to simplify complex expressions and solve equations. By following the steps outlined above, we can factor the expression 4x2 + 28x + 49 and simplify it to (2x + 7)(2x + 7) or (2x + 7)^2. Simplifying expressions has numerous benefits, including making complex expressions easier to work with and reducing errors.
We encourage you to share your thoughts on factoring and its applications in the comments section below. How do you use factoring in your daily life or in your studies?
What is factoring in algebra?
+Factoring in algebra is the process of expressing an algebraic expression as a product of its prime factors, which can be simpler polynomials or even constants.
Why is factoring important in algebra?
+Factoring is important in algebra because it allows us to simplify complex expressions, solve equations, and identify relationships between different variables and constants.
How do I factor a quadratic expression?
+To factor a quadratic expression, check if the expression can be factored, look for two numbers whose product is ac and whose sum is b, and write the expression as a product of two binomials.