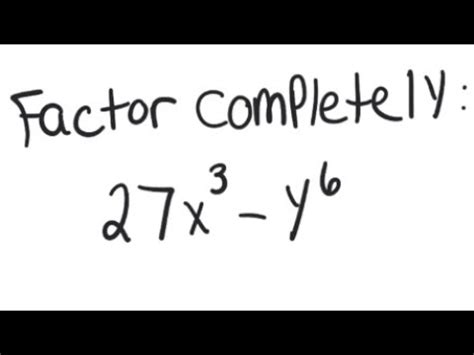The world of algebraic expressions can be complex and overwhelming, especially when it comes to factoring. Factoring expressions is a crucial skill that can help simplify complex equations and make them more manageable. In this article, we will delve into the world of factoring expressions and explore the concept of factoring 27x3+Y6.
What is Factoring?

Factoring is the process of expressing an algebraic expression as a product of simpler expressions, called factors. Factoring is a powerful tool that can help simplify complex equations, solve quadratic equations, and even find the roots of polynomials.
Why is Factoring Important?
Factoring is essential in algebra and is used in a wide range of mathematical applications, including:
- Solving quadratic equations
- Finding the roots of polynomials
- Simplifying complex expressions
- Graphing functions
Factoring Expressions: 27x3+Y6

Now, let's dive into the specific expression 27x3+Y6. This expression is a polynomial expression with two terms: 27x3 and Y6. Our goal is to factor this expression and simplify it.
Step 1: Identify the Greatest Common Factor (GCF)
The first step in factoring is to identify the greatest common factor (GCF) of the two terms. The GCF is the largest factor that divides both terms evenly. In this case, the GCF of 27x3 and Y6 is 3.
Step 2: Factor Out the GCF
Now that we have identified the GCF, we can factor it out of both terms. This means that we can rewrite the expression as:
27x3+Y6 = 3(9x3+2Y2)
Step 3: Factor the Remaining Terms
Next, we can factor the remaining terms, 9x3 and 2Y2. These terms can be factored as:
9x3 = 3(3x2) 2Y2 = 2(Y2)
Step 4: Combine the Factors
Finally, we can combine the factors to get the fully factored expression:
27x3+Y6 = 3(3(3x2)+2(Y2))
Benefits of Factoring

Factoring expressions has several benefits, including:
- Simplifying complex equations
- Solving quadratic equations
- Finding the roots of polynomials
- Graphing functions
Common Mistakes to Avoid

When factoring expressions, there are several common mistakes to avoid, including:
- Forgetting to identify the GCF
- Factoring out the wrong factor
- Not combining the factors correctly
Conclusion: Take Action
In conclusion, factoring expressions is a powerful tool that can help simplify complex equations and make them more manageable. By following the steps outlined in this article, you can learn to factor expressions like 27x3+Y6 and improve your math skills. Don't be afraid to try new things and practice factoring different expressions. With time and practice, you'll become a pro at factoring and be able to tackle even the most complex equations.
We'd love to hear from you! Share your thoughts and questions in the comments below. Have you ever struggled with factoring expressions? What tips and tricks do you have for factoring? Let's discuss!
What is factoring in algebra?
+Factoring in algebra is the process of expressing an algebraic expression as a product of simpler expressions, called factors.
Why is factoring important in algebra?
+Factoring is essential in algebra because it can help simplify complex equations, solve quadratic equations, and even find the roots of polynomials.
How do I factor the expression 27x3+Y6?
+To factor the expression 27x3+Y6, follow these steps: identify the greatest common factor (GCF), factor out the GCF, factor the remaining terms, and combine the factors.