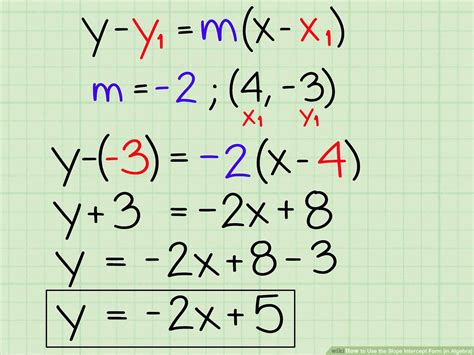Slope Intercept Form Equation Identification Made Easy

Quick Links :

Understanding slope-intercept form equations is a fundamental concept in algebra, and being able to identify and work with them can make a significant difference in solving various math problems. In this article, we will delve into the world of slope-intercept form equations, exploring their structure, benefits, and applications, as well as providing practical examples and steps to make equation identification a breeze.

What is Slope-Intercept Form?

Slope-intercept form is a way of expressing linear equations in the form y = mx + b, where:

• m represents the slope of the line
• b represents the y-intercept (the point where the line crosses the y-axis)
• x is the independent variable
• y is the dependent variable

This form is particularly useful for identifying the slope and y-intercept of a line, which can be crucial in various mathematical and real-world applications.

Benefits of Slope-Intercept Form

There are several benefits to using slope-intercept form equations:

• Easy to identify slope and y-intercept: By simply looking at the equation, you can determine the slope and y-intercept of the line.
• Simplifies graphing: Slope-intercept form makes it easy to graph lines, as you can quickly identify the y-intercept and use the slope to determine the direction of the line.
• Facilitates equation solving: Slope-intercept form can make it easier to solve systems of linear equations, as you can use the slope and y-intercept to identify equivalent equations.

How to Identify Slope-Intercept Form Equations

Identifying slope-intercept form equations can be a straightforward process if you know what to look for. Here are some steps to follow:

1. Check the equation structure: Look for equations in the form y = mx + b, where m and b are constants.
2. Identify the slope: The slope (m) is the coefficient of the x term. A positive slope indicates a line that slopes upward from left to right, while a negative slope indicates a line that slopes downward from left to right.
3. Identify the y-intercept: The y-intercept (b) is the constant term in the equation. This represents the point where the line crosses the y-axis.

Examples of Slope-Intercept Form Equations

Here are a few examples of slope-intercept form equations:

• y = 2x + 3 (slope = 2, y-intercept = 3)
• y = -x - 2 (slope = -1, y-intercept = -2)
• y = 0.5x + 1 (slope = 0.5, y-intercept = 1)

Applications of Slope-Intercept Form Equations

Slope-intercept form equations have numerous applications in various fields, including:

• Physics: Slope-intercept form equations can be used to model the motion of objects, where the slope represents the velocity and the y-intercept represents the initial position.
• Economics: Slope-intercept form equations can be used to model the relationship between variables such as price and demand, where the slope represents the elasticity of demand.
• Computer Science: Slope-intercept form equations can be used in computer graphics to model lines and curves.

Practical Tips for Working with Slope-Intercept Form Equations

Here are some practical tips for working with slope-intercept form equations:

• Use online tools: There are many online tools and calculators that can help you graph and solve slope-intercept form equations.
• Practice, practice, practice: The more you practice working with slope-intercept form equations, the more comfortable you will become with identifying and solving them.
• Pay attention to units: When working with slope-intercept form equations, make sure to pay attention to the units of the variables and constants.

Conclusion

In conclusion, slope-intercept form equations are a fundamental concept in algebra, and being able to identify and work with them can make a significant difference in solving various math problems. By understanding the structure and benefits of slope-intercept form equations, as well as practicing with examples and applications, you can become more confident and proficient in your ability to work with these equations.

We hope this article has been informative and helpful in your understanding of slope-intercept form equations. If you have any questions or comments, please don't hesitate to share them below.