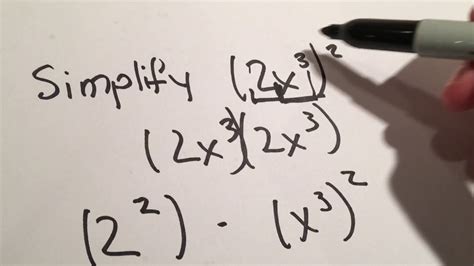Simplifying Expressions: A Key to Unlocking Algebraic Secrets

In the realm of algebra, simplifying expressions is a crucial skill that can help you tackle complex problems with ease. One such expression is X^2 + 2x^3, which may seem daunting at first, but can be simplified in just one easy step.
What is the Importance of Simplifying Expressions?
Before we dive into the simplification process, it's essential to understand why simplifying expressions is vital in algebra. By simplifying expressions, you can:
- Reduce the complexity of the problem, making it easier to solve
- Eliminate unnecessary variables or terms
- Reveal hidden patterns or relationships between variables
- Make it easier to compare or combine expressions
Simplifying X^2 + 2x^3 in 1 Easy Step

Now, let's get to the simplification process. The expression X^2 + 2x^3 can be simplified by factoring out the greatest common factor (GCF). In this case, the GCF is x^2.
X^2 + 2x^3 = x^2(1 + 2x)
Breaking Down the Simplification Process
To simplify the expression, we followed these steps:
- Identify the greatest common factor (GCF) of the terms, which is x^2.
- Factor out the GCF from each term.
- Simplify the expression by combining like terms.
Benefits of Simplifying Expressions

Simplifying expressions has numerous benefits, including:
- Improved problem-solving skills
- Enhanced understanding of algebraic concepts
- Increased confidence in tackling complex problems
- Better time management and reduced frustration
Common Mistakes to Avoid When Simplifying Expressions
When simplifying expressions, it's essential to avoid common mistakes, such as:
- Forgetting to factor out the GCF
- Misidentifying the GCF
- Failing to simplify the expression fully
Practical Applications of Simplifying Expressions

Simplifying expressions has numerous practical applications in various fields, including:
- Physics and engineering, where complex equations need to be simplified to solve problems
- Computer science, where algorithms and data structures rely on simplified expressions
- Economics, where simplified expressions help model complex economic systems
Conclusion
Simplifying expressions is a crucial skill in algebra that can help you unlock complex problems and reveal hidden patterns. By following the simple step outlined above, you can simplify X^2 + 2x^3 and other expressions with ease. Remember to avoid common mistakes and apply simplifying expressions to real-world problems to enhance your problem-solving skills.
What is the importance of simplifying expressions in algebra?
+Simplifying expressions helps reduce complexity, eliminate unnecessary variables or terms, reveal hidden patterns or relationships between variables, and make it easier to compare or combine expressions.
How do I simplify the expression X^2 + 2x^3?
+Factor out the greatest common factor (GCF), which is x^2, and simplify the expression to x^2(1 + 2x).
What are the benefits of simplifying expressions?
+Simplifying expressions improves problem-solving skills, enhances understanding of algebraic concepts, increases confidence in tackling complex problems, and reduces frustration.