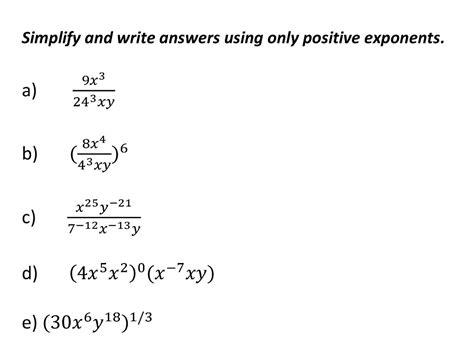Simplifying Exponents: 8x4, 8x8, 32x4, 32x8 Made Easy

Quick Links :

Have you ever struggled with simplifying exponents? You're not alone! Many students find it challenging to work with exponents, especially when dealing with larger numbers. In this article, we'll explore how to simplify exponents like 8x4, 8x8, 32x4, and 32x8, making it easier for you to understand and solve.

Understanding Exponents

Before we dive into simplifying exponents, it's essential to understand what exponents are and how they work. Exponents are shorthand notation for repeated multiplication. For example, 2^3 means 2 multiplied by itself three times: 2 × 2 × 2 = 8. In this case, 2 is the base, and 3 is the exponent.

Simplifying Exponents: Rules and Examples

To simplify exponents, you need to follow some basic rules:

• Product of Powers: When multiplying two numbers with the same base, add the exponents. For example, 2^3 × 2^4 = 2^(3+4) = 2^7.
• Power of a Power: When raising a number with an exponent to another power, multiply the exponents. For example, (2^3)^4 = 2^(3×4) = 2^12.
• Quotient of Powers: When dividing two numbers with the same base, subtract the exponents. For example, 2^5 ÷ 2^3 = 2^(5-3) = 2^2.

Let's apply these rules to simplify the given exponents:

• 8x4: Since 8 can be expressed as 2^3, we have (2^3)^4 = 2^(3×4) = 2^12.
• 8x8: Using the same logic as above, we get (2^3)^8 = 2^(3×8) = 2^24.
• 32x4: Since 32 can be expressed as 2^5, we have (2^5)^4 = 2^(5×4) = 2^20.
• 32x8: Similarly, we get (2^5)^8 = 2^(5×8) = 2^40.

Example Problems

• Simplify (3^2)^5: Using the power of a power rule, we get 3^(2×5) = 3^10.
• Simplify 2^8 ÷ 2^3: Using the quotient of powers rule, we get 2^(8-3) = 2^5.
• Simplify (5^3)^2: Using the power of a power rule, we get 5^(3×2) = 5^6.

Real-World Applications of Exponents

Exponents have numerous applications in real-world scenarios, including:

• Finance: Compound interest, investment growth, and inflation rates often involve exponents.
• Science: Exponents are used to describe population growth, chemical reactions, and radioactive decay.
• Computer Science: Exponents are used in algorithms, data compression, and cryptography.

In conclusion, simplifying exponents might seem daunting at first, but with the right rules and practice, it becomes easier. We hope this article has helped you understand and simplify exponents like 8x4, 8x8, 32x4, and 32x8. Do you have any questions or topics you'd like to discuss? Share your thoughts in the comments below!

Exponent Simplification Tips

• Use the Rules: Familiarize yourself with the product of powers, power of a power, and quotient of powers rules.
• Break Down Complex Problems: Divide complex problems into simpler ones using the rules of exponents.
• Practice, Practice, Practice: The more you practice simplifying exponents, the more comfortable you'll become.

We hope you found this article helpful in understanding and simplifying exponents. Share your favorite exponent simplification tips in the comments below!