Mastering Quadratic Equations: What Is Standard Form

Quick Links :

Mastering quadratic equations is a crucial milestone in algebra, and understanding the standard form is the first step towards achieving this goal. Quadratic equations are used to describe a wide range of phenomena in physics, engineering, economics, and computer science, making them an essential tool for problem-solving in these fields. In this article, we will delve into the world of quadratic equations, explore the standard form, and provide practical examples to help you master this fundamental concept.

What Are Quadratic Equations?

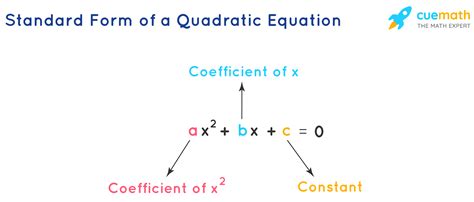
Quadratic equations are polynomial equations of degree two, which means the highest power of the variable (usually x) is two. They have the general form of ax^2 + bx + c = 0, where a, b, and c are constants, and a cannot be zero. Quadratic equations can be solved using various methods, including factoring, completing the square, and using the quadratic formula.

Why Is Standard Form Important?

Standard form is the most common way to write quadratic equations, and it provides a clear and concise way to represent the equation. The standard form of a quadratic equation is ax^2 + bx + c = 0, where a, b, and c are constants, and a cannot be zero. This form is useful for several reasons:

• It allows us to easily identify the coefficients of the equation.
• It provides a clear and concise way to represent the equation.
• It makes it easier to solve the equation using various methods.
• It helps us to identify the type of quadratic equation we are dealing with.

Types of Quadratic Equations

There are several types of quadratic equations, including:

• Linear quadratic equations: These are quadratic equations that can be factored into the product of two linear factors.
• Quadratic equations with complex roots: These are quadratic equations that have complex roots, which cannot be factored into the product of two linear factors.
• Quadratic equations with real roots: These are quadratic equations that have real roots, which can be factored into the product of two linear factors.

How to Write Quadratic Equations in Standard Form

To write a quadratic equation in standard form, follow these steps:

1. Identify the coefficients of the equation.
2. Rearrange the equation to have the terms in the correct order.
3. Factor out any common factors.

For example, consider the equation x^2 + 5x = 0. To write this equation in standard form, we need to add a constant term to both sides of the equation. Let's add 1 to both sides:

x^2 + 5x + 1 = 1

Now, we can rearrange the equation to have the terms in the correct order:

x^2 + 5x + 1 = 1

This is the standard form of the equation.

Practical Examples

Here are some practical examples of writing quadratic equations in standard form:

• Example 1: Write the equation x^2 - 4x = 0 in standard form.
• Example 2: Write the equation x^2 + 2x - 6 = 0 in standard form.
• Example 3: Write the equation x^2 - 3x - 2 = 0 in standard form.

Benefits of Mastering Quadratic Equations

Mastering quadratic equations has numerous benefits, including:

• Improved problem-solving skills: Quadratic equations are used to model a wide range of real-world phenomena, and mastering them can help you develop strong problem-solving skills.
• Enhanced analytical skills: Quadratic equations require analytical thinking, and mastering them can help you develop your analytical skills.
• Increased confidence: Mastering quadratic equations can boost your confidence in math and help you tackle more challenging problems.

Conclusion: Mastering Quadratic Equations Takes Practice

Mastering quadratic equations takes practice, patience, and persistence. With the standard form as your foundation, you can build a strong understanding of quadratic equations and develop the skills you need to tackle more challenging problems. Remember to practice regularly, and don't be afraid to ask for help when you need it. With time and effort, you can master quadratic equations and unlock the doors to a wide range of mathematical and scientific applications.