60 Percent In Fraction Form Explained

Quick Links :

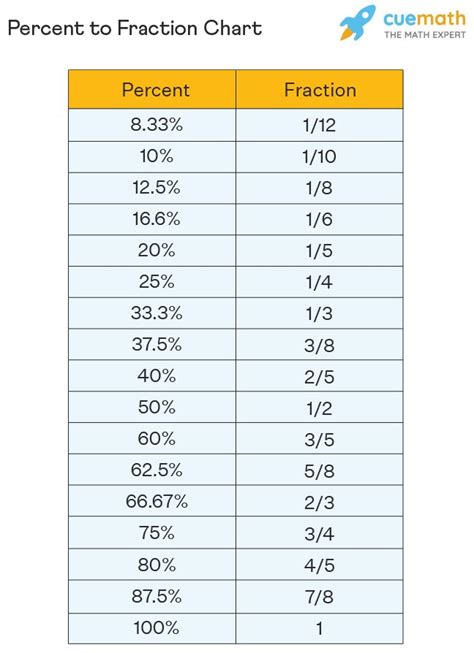
Converting percentages to fractions is an essential skill in mathematics, and understanding this concept can make a significant difference in various calculations and problem-solving situations. One of the most common percentages that people encounter is 60 percent. In this article, we will delve into the world of fractions and explore how to express 60 percent in fraction form.

The Importance of Converting Percentages to Fractions

Before we dive into the specifics of converting 60 percent to a fraction, it's essential to understand why this conversion is crucial. Percentages are a way to express a value as a fraction of 100. However, in many mathematical operations, it's more convenient to work with fractions rather than percentages. Fractions provide a more intuitive understanding of proportions and can simplify calculations. Moreover, fractions are essential in various mathematical concepts, such as algebra, geometry, and calculus.

Converting 60 Percent to a Fraction

To convert 60 percent to a fraction, we need to express it as a ratio of two numbers. The percentage sign (%) indicates that the value is a fraction of 100. Therefore, we can write 60 percent as:

60% = 60/100

Now, we can simplify this fraction by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 20.

60 ÷ 20 = 3 100 ÷ 20 = 5

So, the simplified fraction is:

3/5

This means that 60 percent is equivalent to the fraction 3/5.

Real-World Applications of 60 Percent as a Fraction

Now that we know how to express 60 percent as a fraction, let's explore some real-world scenarios where this conversion is useful. Here are a few examples:

• Cooking: Recipes often involve proportions, and converting percentages to fractions can simplify the process. For instance, if a recipe requires 60% of a cup of flour, you can convert it to 3/5 of a cup.
• Finance: In finance, percentages are commonly used to express interest rates, returns on investment, and discounts. Converting these percentages to fractions can help you better understand the proportions involved. For example, if an investment returns 60% per annum, you can express it as a fraction (3/5) to calculate the returns more easily.
• Science: In scientific calculations, percentages are often used to express concentrations, proportions, and ratios. Converting these percentages to fractions can simplify the calculations and provide a more intuitive understanding of the proportions involved.

Working with Fractions: Tips and Tricks

Now that we've explored the concept of converting 60 percent to a fraction, let's discuss some tips and tricks for working with fractions:

• Simplifying fractions: Always simplify fractions by dividing both the numerator and the denominator by their GCD.
• Comparing fractions: To compare fractions, convert them to equivalent fractions with the same denominator.
• Adding and subtracting fractions: To add or subtract fractions, ensure they have the same denominator. Then, add or subtract the numerators.

Fraction Operations: A Step-by-Step Guide

Here's a step-by-step guide to performing common fraction operations:

1. Adding fractions:
   • Ensure the fractions have the same denominator.
   • Add the numerators.
   • Keep the same denominator.
2. Subtracting fractions:
   • Ensure the fractions have the same denominator.
   • Subtract the numerators.
   • Keep the same denominator.
3. Multiplying fractions:
   • Multiply the numerators.
   • Multiply the denominators.
   • Simplify the resulting fraction.
4. Dividing fractions:
   • Invert the second fraction (i.e., flip the numerator and denominator).
   • Multiply the fractions.

Conclusion and Next Steps

In this article, we've explored the concept of converting 60 percent to a fraction and discussed the importance of working with fractions in various mathematical operations. We've also provided tips and tricks for simplifying fractions, comparing fractions, and performing common fraction operations.

If you're interested in learning more about fractions and percentages, we recommend exploring the following topics:

• Equivalent ratios: Learn how to identify and create equivalent ratios.
• Proportional relationships: Understand how to identify and graph proportional relationships.
• Percent increase and decrease: Learn how to calculate percent increase and decrease.

By mastering these concepts, you'll become more proficient in working with fractions and percentages, and you'll be better equipped to tackle various mathematical challenges.