Understanding Fractions: A Fundamental Math Concept

Fractions are a crucial part of mathematics, and understanding them is essential for various mathematical operations. A fraction is a way to express a part of a whole as a ratio of two numbers. In this article, we will delve into the world of fractions, exploring what they are, how to work with them, and their significance in mathematics.
What is a Fraction?
A fraction is a mathematical expression that represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator tells us how many equal parts we have, while the denominator tells us how many parts the whole is divided into.
For example, the fraction 3/4 represents three equal parts out of a total of four parts. In other words, if we have a pizza that is divided into four equal slices, and we eat three of them, we can represent this as 3/4 of the pizza.
Types of Fractions

There are several types of fractions, each with its own unique characteristics.
- Proper Fractions: A proper fraction is a fraction where the numerator is less than the denominator. For example, 3/4 is a proper fraction.
- Improper Fractions: An improper fraction is a fraction where the numerator is greater than or equal to the denominator. For example, 4/3 is an improper fraction.
- Mixed Fractions: A mixed fraction is a combination of a whole number and a proper fraction. For example, 2 3/4 is a mixed fraction.
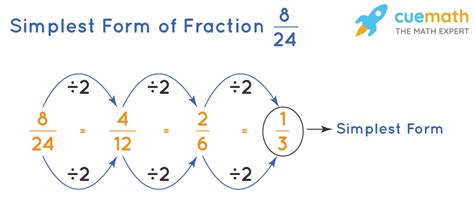
- Equivalent Fractions: Equivalent fractions are fractions that have the same value, but with different numerators and denominators. For example, 1/2 and 2/4 are equivalent fractions.
Working with Fractions
Fractions can be added, subtracted, multiplied, and divided, just like whole numbers. However, the rules for working with fractions are slightly different.
- Adding and Subtracting Fractions: To add or subtract fractions, we need to have the same denominator. We can then add or subtract the numerators, while keeping the denominator the same.
- Multiplying Fractions: To multiply fractions, we multiply the numerators and multiply the denominators.
- Dividing Fractions: To divide fractions, we invert the second fraction (i.e., flip the numerator and denominator) and then multiply.
Real-World Applications of Fractions

Fractions have numerous real-world applications, from cooking and measuring ingredients to finance and calculating interest rates. They are also essential in various mathematical concepts, such as algebra and geometry.
In conclusion, fractions are a fundamental part of mathematics, and understanding them is crucial for various mathematical operations. By recognizing the different types of fractions and learning how to work with them, we can unlock a deeper understanding of mathematics and its many applications.
What's Next?
Now that you have a better understanding of fractions, try practicing with some simple fraction problems. You can also explore more advanced mathematical concepts, such as equivalent ratios and proportionality.
Share Your Thoughts!
Do you have any questions or comments about fractions? Share them with us in the comments section below!
FAQ Section
What is the difference between a proper fraction and an improper fraction?
+A proper fraction is a fraction where the numerator is less than the denominator, while an improper fraction is a fraction where the numerator is greater than or equal to the denominator.
How do I add fractions with different denominators?
+To add fractions with different denominators, you need to find the least common multiple (LCM) of the denominators and then convert each fraction to have the LCM as the denominator.
What is the significance of equivalent fractions?
+Equivalent fractions are fractions that have the same value, but with different numerators and denominators. They are essential in various mathematical concepts, such as equivalent ratios and proportionality.