What Is Standard Form Of A Quadratic Function

Quick Links :

Quadratic functions are a fundamental concept in algebra and mathematics, and understanding their standard form is crucial for solving equations and graphing curves. In this article, we will delve into the world of quadratic functions, explore their standard form, and discuss the benefits and applications of this essential mathematical concept.

What is a Quadratic Function?

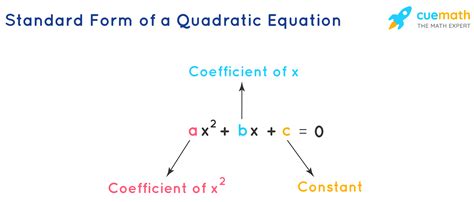
A quadratic function is a polynomial function of degree two, which means the highest power of the variable (usually x) is two. The general form of a quadratic function is:

f(x) = ax^2 + bx + c

where a, b, and c are constants, and x is the variable. The coefficient "a" is called the leading coefficient, "b" is the linear coefficient, and "c" is the constant term.

What is the Standard Form of a Quadratic Function?

The standard form of a quadratic function is:

f(x) = a(x - h)^2 + k

where (h, k) is the vertex of the parabola. This form is also known as the vertex form. The standard form is useful for identifying the vertex, axis of symmetry, and the direction of the parabola's opening.

How to Convert a Quadratic Function to Standard Form

To convert a quadratic function from its general form to standard form, you need to complete the square. Here's a step-by-step guide:

1. Factor out the leading coefficient (a) from the first two terms: f(x) = a(x^2 + (b/a)x) + c
2. Add and subtract (b/2a)^2 inside the parentheses: f(x) = a(x^2 + (b/a)x + (b/2a)^2 - (b/2a)^2) + c
3. Simplify the expression: f(x) = a(x + (b/2a))^2 - (b^2/4a) + c
4. Combine the constants: f(x) = a(x + (b/2a))^2 + (c - b^2/4a)

The resulting expression is in standard form, where h = -b/2a and k = c - b^2/4a.

Benefits of Standard Form

The standard form of a quadratic function has several benefits:

• Easy identification of the vertex: The standard form allows you to identify the vertex (h, k) of the parabola, which is essential for graphing and solving equations.
• Axis of symmetry: The standard form helps you find the axis of symmetry, which is the vertical line x = h.
• Direction of opening: The standard form indicates whether the parabola opens upwards (a > 0) or downwards (a < 0).
• Simplifies graphing: The standard form makes it easier to graph quadratic functions, as you can identify the vertex and axis of symmetry.

Applications of Quadratic Functions

Quadratic functions have numerous real-world applications:

• Physics and engineering: Quadratic functions are used to model the motion of objects, including projectile motion and the trajectory of a thrown ball.
• Economics: Quadratic functions are used to model supply and demand curves, as well as the behavior of markets.
• Computer science: Quadratic functions are used in algorithms for solving systems of equations and optimization problems.
• Data analysis: Quadratic functions are used to model and analyze data in fields such as finance, biology, and social sciences.

Common Mistakes to Avoid

When working with quadratic functions, here are some common mistakes to avoid:

• Incorrectly identifying the vertex: Make sure to complete the square correctly to identify the vertex.
• Forgetting to include the leading coefficient: Remember to include the leading coefficient (a) when writing the standard form.
• Confusing the axis of symmetry: The axis of symmetry is the vertical line x = h, not the horizontal line y = k.

Conclusion

In conclusion, understanding the standard form of a quadratic function is essential for solving equations, graphing curves, and applying mathematical concepts to real-world problems. By completing the square and converting quadratic functions to standard form, you can identify the vertex, axis of symmetry, and direction of opening. Remember to avoid common mistakes and practice working with quadratic functions to become proficient in this fundamental mathematical concept.