One-Third Of One-Third In Fraction Form

Quick Links :

Understanding Fractions and Simplifying Complex Ratios

In the world of mathematics, fractions are a fundamental concept that allows us to express part of a whole. They are used in various mathematical operations, such as addition, subtraction, multiplication, and division. When dealing with complex ratios, it's essential to understand how to simplify them. In this article, we'll explore the concept of one-third of one-third in fraction form and provide a step-by-step guide on how to simplify it.

What is a Fraction?

A fraction is a mathematical expression that represents a part of a whole. It consists of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator tells us how many equal parts we have, while the denominator tells us how many parts the whole is divided into. For example, in the fraction 3/4, the numerator is 3, and the denominator is 4.

Understanding the Concept of One-Third

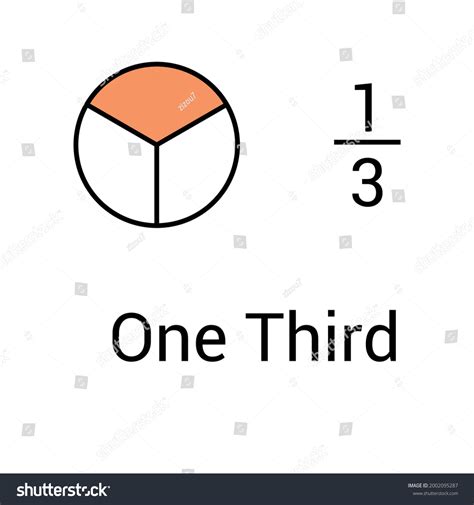
One-third is a fraction that represents one part out of three equal parts. It can be expressed mathematically as 1/3. In everyday life, we use one-third to describe a portion of something, such as one-third of a pizza or one-third of a tank of gas.

What is One-Third of One-Third?

When we talk about one-third of one-third, we're essentially asking for a fraction of a fraction. To calculate this, we need to multiply the two fractions together. The mathematical expression for one-third of one-third is (1/3) × (1/3).

Calculating One-Third of One-Third

To calculate one-third of one-third, we multiply the two fractions together:

(1/3) × (1/3) = 1/9

So, one-third of one-third is equal to 1/9.

Practical Applications of One-Third of One-Third

One-third of one-third may seem like a complex concept, but it has practical applications in real-life scenarios. For example, imagine you have a pizza that's divided into three equal parts, and each part is further divided into three smaller parts. If you take one of those smaller parts, you'll have one-third of one-third of the pizza.

Simplifying Complex Ratios

When dealing with complex ratios, it's essential to simplify them to make calculations easier. Here are some steps to simplify complex ratios:

1. Identify the fractions: Break down the complex ratio into individual fractions.
2. Multiply the fractions: Multiply the fractions together to get the result.
3. Simplify the result: Simplify the resulting fraction by dividing both the numerator and denominator by their greatest common divisor (GCD).

Real-Life Examples of Simplifying Complex Ratios

Simplifying complex ratios is a crucial skill in various fields, such as science, engineering, and finance. Here are some real-life examples:

• A recipe calls for 2/3 cup of flour, but you only have a 1/4 cup measuring cup. To calculate the number of cups you need, you'll need to simplify the complex ratio.
• A company has a profit margin of 1/5, and you want to calculate the profit margin of a specific product that has a 1/3 markup. To do this, you'll need to simplify the complex ratio.

Conclusion: One-Third of One-Third in Fraction Form

In conclusion, one-third of one-third is a complex ratio that can be simplified to 1/9. Understanding fractions and simplifying complex ratios are essential skills in mathematics and real-life applications. By following the steps outlined in this article, you'll be able to simplify complex ratios and make calculations easier.

Get Involved!

We'd love to hear from you! Share your thoughts on simplifying complex ratios and provide examples of how you've used this skill in real-life scenarios. Don't forget to comment below and share this article with your friends and family.