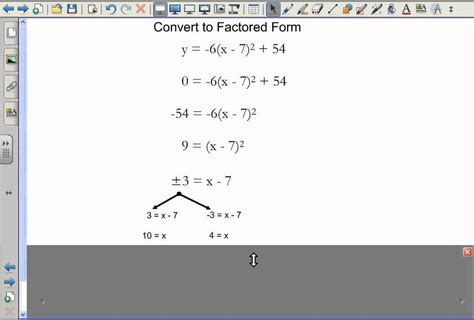
Vertex form is a quadratic equation written in the form f(x) = a(x - h)^2 + k, where (h, k) represents the vertex of the parabola. Converting a quadratic equation to vertex form can be a bit challenging, but with the right steps, you can easily transform any quadratic equation into factored form.
The importance of converting to vertex form lies in its ability to provide valuable information about the parabola, such as its vertex, axis of symmetry, and the direction of the parabola's opening. Moreover, vertex form makes it easier to graph the parabola and identify its key features.
In this article, we will explore the steps to convert a quadratic equation to factored form, along with practical examples and explanations to help you understand the process.
Why Convert to Vertex Form?
Before diving into the conversion process, let's discuss the benefits of converting a quadratic equation to vertex form.

Converting to vertex form allows you to:
- Easily identify the vertex and axis of symmetry
- Determine the direction of the parabola's opening
- Graph the parabola with precision
- Solve quadratic equations more efficiently
Step-by-Step Conversion Process
To convert a quadratic equation to factored form, follow these steps:
Step 1: Write the Quadratic Equation
Start by writing the quadratic equation in standard form: f(x) = ax^2 + bx + c.
Example: f(x) = x^2 + 5x + 6
Step 2: Complete the Square
To complete the square, you'll need to manipulate the equation to create a perfect square trinomial. To do this:
- Take half of the coefficient of x (b/2a) and square it
- Add and subtract the result within the parentheses
- Simplify the equation
Example:
x^2 + 5x + 6 = (x^2 + 5x + (5/2)^2) - (5/2)^2 + 6
Simplify:
x^2 + 5x + 6 = (x + 5/2)^2 - 25/4 + 6
Combine like terms:
x^2 + 5x + 6 = (x + 5/2)^2 - 1/4
Step 3: Write in Factored Form
The equation is now in vertex form: f(x) = a(x - h)^2 + k.
Identify the values of a, h, and k:
a = 1, h = -5/2, k = -1/4
Write the equation in factored form:
f(x) = (x + 5/2)^2 - 1/4
Tips and Tricks
- Make sure to simplify the equation thoroughly to avoid errors
- Pay attention to the signs and coefficients to ensure accurate conversion
- Use online tools or calculators to verify your results, if needed
Example 2: Convert to Factored Form
Convert the quadratic equation x^2 - 3x - 4 to factored form.
Follow the steps:
Step 1: Write the Quadratic Equation
f(x) = x^2 - 3x - 4
Step 2: Complete the Square
x^2 - 3x - 4 = (x^2 - 3x + (-3/2)^2) - (-3/2)^2 - 4
Simplify:
x^2 - 3x - 4 = (x - 3/2)^2 - 9/4 - 4
Combine like terms:
x^2 - 3x - 4 = (x - 3/2)^2 - 25/4
Step 3: Write in Factored Form
Identify the values of a, h, and k:
a = 1, h = 3/2, k = -25/4
Write the equation in factored form:
f(x) = (x - 3/2)^2 - 25/4

Conclusion: Mastering Vertex Form Conversion
Converting a quadratic equation to factored form may seem daunting, but with practice and patience, you'll become proficient in this skill. Remember to follow the step-by-step process, simplify thoroughly, and pay attention to signs and coefficients.
Take a moment to practice converting a few quadratic equations to factored form. You can use online tools or calculators to verify your results.
Share your thoughts and experiences with converting to vertex form in the comments below. Do you have any questions or need further clarification on any of the steps?