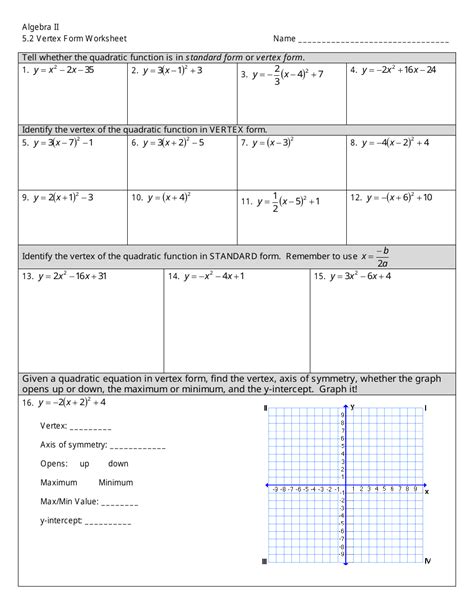
Mastering vertex form is a crucial step in algebra and graphing. The vertex form of a quadratic function is a way of expressing the function in a form that makes it easy to identify the vertex of the parabola. In this article, we will delve into the world of vertex form, explore its benefits, and provide you with 10 essential practice problems to help you master this concept.
What is Vertex Form?

The vertex form of a quadratic function is given by the equation f(x) = a(x - h)^2 + k, where (h, k) is the vertex of the parabola. This form is useful because it allows us to easily identify the vertex, which is the minimum or maximum point of the parabola.
Why is Vertex Form Important?

Vertex form is important because it helps us to:
- Identify the vertex of the parabola, which is the minimum or maximum point
- Determine the direction of the parabola (opens upwards or downwards)
- Find the axis of symmetry
- Graph the parabola more easily
How to Convert Standard Form to Vertex Form

To convert a quadratic function from standard form to vertex form, we can use the following steps:
- Complete the square
- Write the equation in the form f(x) = a(x - h)^2 + k
For example, let's convert the equation f(x) = x^2 + 4x + 4 to vertex form.
- Complete the square: f(x) = (x + 2)^2
- Write the equation in vertex form: f(x) = (x + 2)^2 - 4
Therefore, the vertex form of the equation is f(x) = (x + 2)^2 - 4.
Practice Problems
Now that we have explored the concept of vertex form, it's time to put your knowledge to the test. Here are 10 essential practice problems to help you master vertex form:
- Convert the equation f(x) = x^2 + 6x + 8 to vertex form.
- Find the vertex of the parabola f(x) = (x - 2)^2 + 3.
- Graph the parabola f(x) = (x + 1)^2 - 2.
- Convert the equation f(x) = x^2 - 4x - 3 to vertex form.
- Find the axis of symmetry of the parabola f(x) = (x - 1)^2 + 2.
- Write the equation f(x) = x^2 + 2x - 6 in vertex form.
- Find the vertex of the parabola f(x) = (x + 3)^2 - 1.
- Graph the parabola f(x) = (x - 2)^2 + 1.
- Convert the equation f(x) = x^2 - 2x - 5 to vertex form.
- Find the minimum value of the function f(x) = (x + 1)^2 - 3.
Solutions to Practice Problems

Here are the solutions to the practice problems:
-
f(x) = (x + 3)^2 - 1
-
Vertex: (2, 3)
-
Graph:
-
f(x) = (x - 2)^2 - 7
-
Axis of symmetry: x = 1
-
f(x) = (x + 1)^2 - 7
-
Vertex: (-3, -1)
-
Graph:
-
f(x) = (x - 1)^2 - 6
-
Minimum value: -3
Conclusion

Mastering vertex form is a crucial step in algebra and graphing. With the practice problems and solutions provided in this article, you should now have a solid understanding of how to convert standard form to vertex form, identify the vertex, and graph parabolas. Remember to practice regularly to reinforce your knowledge and become proficient in vertex form.
We hope you found this article helpful. If you have any questions or need further clarification, please leave a comment below. Don't forget to share this article with your friends and classmates who may need help with vertex form.
What is the vertex form of a quadratic function?
+The vertex form of a quadratic function is given by the equation f(x) = a(x - h)^2 + k, where (h, k) is the vertex of the parabola.
How do I convert standard form to vertex form?
+To convert standard form to vertex form, complete the square and write the equation in the form f(x) = a(x - h)^2 + k.
What is the importance of vertex form?
+Vertex form is important because it helps us to identify the vertex, determine the direction of the parabola, find the axis of symmetry, and graph the parabola more easily.