5 Ways To Master Vector Trigonometric Form

Quick Links :

Mastering vector trigonometric form is an essential skill for students of mathematics, physics, and engineering. It provides a powerful tool for representing and analyzing complex numbers and periodic phenomena. In this article, we will explore five ways to master vector trigonometric form, including understanding the basics, visualizing complex numbers, using trigonometric identities, applying vector operations, and practicing with real-world examples.

Understanding the Basics of Vector Trigonometric Form

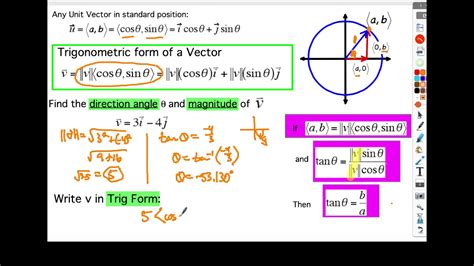
Vector trigonometric form is a way of representing complex numbers in terms of their magnitude and direction. It is based on the concept of trigonometry, which is the study of triangles and their relationships. In vector trigonometric form, a complex number is represented as a vector in the complex plane, with its magnitude (length) and direction (angle) defined by trigonometric functions.

To understand the basics of vector trigonometric form, it is essential to recall the fundamental concepts of trigonometry, including sine, cosine, and tangent. These functions relate the angles and side lengths of triangles and are used to define the magnitude and direction of complex numbers.

Defining Complex Numbers in Vector Trigonometric Form

A complex number can be represented in vector trigonometric form as:

z = r(cosθ + isinθ)

where z is the complex number, r is the magnitude (length), θ is the direction (angle), and i is the imaginary unit.

Visualizing Complex Numbers in Vector Trigonometric Form

Visualizing complex numbers in vector trigonometric form is crucial for understanding their behavior and relationships. The complex plane is a graphical representation of complex numbers, with the real axis representing the real part and the imaginary axis representing the imaginary part.

By plotting complex numbers in the complex plane, you can visualize their magnitude and direction, making it easier to perform operations and analyze their behavior.

Using the Complex Plane to Visualize Complex Numbers

The complex plane is a powerful tool for visualizing complex numbers. By plotting a complex number in the complex plane, you can:

• Determine its magnitude (length) and direction (angle)
• Identify its real and imaginary parts
• Perform operations, such as addition and multiplication

Using Trigonometric Identities to Simplify Vector Trigonometric Form

Trigonometric identities are equations that relate trigonometric functions to each other. They can be used to simplify vector trigonometric form expressions and perform operations more efficiently.

Some common trigonometric identities used in vector trigonometric form include:

• sin(θ + φ) = sinθcosφ + cosθsinφ
• cos(θ + φ) = cosθcosφ - sinθsinφ
• tan(θ + φ) = (tanθ + tanφ) / (1 - tanθtanφ)

By applying these identities, you can simplify complex expressions and perform operations more easily.

Applying Vector Operations in Vector Trigonometric Form

Vector operations, such as addition and multiplication, can be performed in vector trigonometric form. These operations are essential for analyzing and manipulating complex numbers.

Some common vector operations in vector trigonometric form include:

• Addition: z1 + z2 = (r1cosθ1 + isinθ1) + (r2cosθ2 + isinθ2)
• Multiplication: z1z2 = (r1cosθ1 + isinθ1)(r2cosθ2 + isinθ2)

By applying these operations, you can analyze and manipulate complex numbers in vector trigonometric form.

Practicing with Real-World Examples

Practicing with real-world examples is essential for mastering vector trigonometric form. By applying vector trigonometric form to real-world problems, you can develop a deeper understanding of complex numbers and their behavior.

Some examples of real-world applications of vector trigonometric form include:

• Electrical engineering: analyzing AC circuits and filter design
• Signal processing: representing and analyzing periodic signals
• Navigation: determining distances and directions in navigation systems

By practicing with real-world examples, you can develop your skills in vector trigonometric form and apply them to a wide range of applications.

We hope this article has helped you master vector trigonometric form. Remember to practice with real-world examples and apply vector trigonometric form to a wide range of applications. Share your thoughts and experiences with us in the comments section below!