Vector Form Physics Explained Simply

Quick Links :

Hide

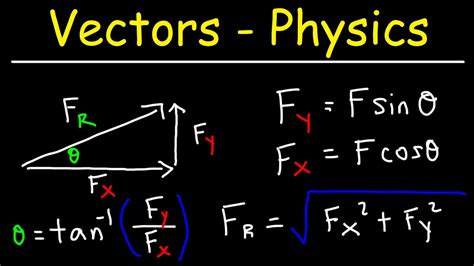
Vectors are a fundamental concept in physics, used to describe quantities with both magnitude (amount of something) and direction. Understanding vectors is crucial for analyzing and solving problems in mechanics, electromagnetism, and other areas of physics. In this article, we will delve into the world of vectors, explaining the basics, types, operations, and applications of vector form physics in a simple and easy-to-understand manner.

What are Vectors?

A vector is a mathematical object that has both magnitude (length) and direction. It can be represented graphically as an arrow in a coordinate system, with the length of the arrow corresponding to the magnitude and the direction of the arrow corresponding to the direction of the vector. Vectors are often denoted by boldface letters, such as a or F.

Types of Vectors

There are several types of vectors, including:

• Displacement vectors: Represent the change in position of an object.
• Velocity vectors: Represent the rate of change of an object's position.
• Acceleration vectors: Represent the rate of change of an object's velocity.
• Force vectors: Represent the push or pull on an object.
• Unit vectors: Vectors with a magnitude of 1, used to represent direction.

Vector Operations

Vectors can be added, subtracted, multiplied, and divided using various operations. Some common vector operations include:

• Vector addition: The sum of two or more vectors, resulting in a new vector.
• Vector subtraction: The difference between two vectors, resulting in a new vector.
• Scalar multiplication: The product of a vector and a scalar (number), resulting in a new vector.
• Dot product: The product of two vectors, resulting in a scalar value.
• Cross product: The product of two vectors, resulting in a new vector.

Vector Addition and Subtraction

Vector addition and subtraction are performed by combining the corresponding components of the vectors. For example, if we have two vectors a = (a1, a2, a3) and b = (b1, b2, b3), the sum of the vectors is:

a + b = (a1 + b1, a2 + b2, a3 + b3)

Similarly, the difference between the vectors is:

a - b = (a1 - b1, a2 - b2, a3 - b3)

Vector Applications in Physics

Vectors are used extensively in physics to describe the motion of objects, forces, and energies. Some examples of vector applications in physics include:

• Projectile motion: Vectors are used to describe the trajectory of projectiles, including the initial velocity, acceleration, and range.
• Force and Newton's laws: Vectors are used to describe the forces acting on an object, including the normal force, frictional force, and gravitational force.
• Energy and work: Vectors are used to describe the energy and work done by forces on an object.
• Electromagnetism: Vectors are used to describe the electric and magnetic fields, including the electric field strength and magnetic field strength.

Real-World Examples of Vector Applications

Vectors are used in many real-world applications, including:

• GPS navigation: Vectors are used to calculate the position and velocity of GPS satellites and receivers.
• Computer graphics: Vectors are used to create 3D models and animations.
• Video games: Vectors are used to simulate the motion of objects and characters.
• Engineering: Vectors are used to design and analyze structures, including bridges and buildings.

Conclusion

Vectors are a fundamental concept in physics, used to describe quantities with both magnitude and direction. Understanding vectors is crucial for analyzing and solving problems in mechanics, electromagnetism, and other areas of physics. By mastering vector form physics, you can gain a deeper understanding of the world around you and develop problem-solving skills that can be applied to a wide range of fields.