Mastering Trinomial Standard Form In 5 Easy Steps

Quick Links :

The concept of trinomial standard form is a fundamental aspect of algebra, and it is essential for students to master it to succeed in their mathematical pursuits. Trinomials are polynomial expressions that consist of three terms, and writing them in standard form is crucial for solving equations, graphing functions, and performing various algebraic operations. In this article, we will guide you through the process of mastering trinomial standard form in five easy steps.

Step 1: Understand the Concept of Trinomials

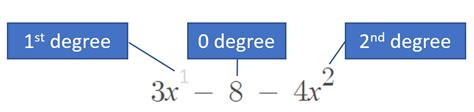
A trinomial is a polynomial expression that consists of three terms, each separated by a plus or minus sign. The general form of a trinomial is ax^2 + bx + c, where a, b, and c are constants, and x is the variable. For example, x^2 + 4x + 4 is a trinomial expression.

To write a trinomial in standard form, we need to ensure that the terms are arranged in a specific order. The standard form of a trinomial is ax^2 + bx + c, where a is the coefficient of the quadratic term, b is the coefficient of the linear term, and c is the constant term.

Key Characteristics of Trinomials

• Trinomials have three terms.
• Each term is separated by a plus or minus sign.
• The terms are arranged in a specific order: quadratic, linear, and constant.

Step 2: Learn the Rules for Writing Trinomials in Standard Form

To write a trinomial in standard form, we need to follow some specific rules:

• The quadratic term (ax^2) must come first.
• The linear term (bx) must come second.
• The constant term (c) must come last.
• The terms must be arranged in descending order of exponents.

For example, the trinomial x^2 + 4x + 4 is already in standard form. However, if we have a trinomial like 4 + 2x + x^2, we need to rearrange the terms to write it in standard form: x^2 + 2x + 4.

Common Mistakes to Avoid

• Writing the terms in the wrong order.
• Omitting the coefficient of the quadratic term.
• Writing the constant term before the linear term.

Step 3: Practice Writing Trinomials in Standard Form

Now that we have learned the rules for writing trinomials in standard form, it's time to practice. Let's consider some examples:

• Write the trinomial 3 + 2x + x^2 in standard form.
• Write the trinomial x^2 - 2x - 3 in standard form.
• Write the trinomial 2x^2 + 5 - 3x in standard form.

By practicing these examples, we can reinforce our understanding of the rules for writing trinomials in standard form.

Benefits of Practicing

• Improves our understanding of the rules.
• Enhances our ability to write trinomials in standard form.
• Prepares us for solving equations and graphing functions.

Step 4: Learn to Factor Trinomials

Factoring trinomials is an essential skill in algebra, and it requires us to write trinomials in standard form. When we factor a trinomial, we express it as a product of two binomials. For example, the trinomial x^2 + 5x + 6 can be factored as (x + 3)(x + 2).

To factor a trinomial, we need to find two numbers whose product is the constant term and whose sum is the coefficient of the linear term. These numbers are called the factors of the trinomial.

Key Steps for Factoring Trinomials

• Write the trinomial in standard form.
• Find the factors of the constant term.
• Find the factors of the linear term.
• Write the factored form of the trinomial.

Step 5: Apply Trinomial Standard Form in Real-World Applications

Trinomial standard form has numerous applications in real-world scenarios, such as physics, engineering, and economics. By mastering trinomial standard form, we can solve problems involving quadratic equations, graph functions, and optimize systems.

For example, in physics, we can use trinomial standard form to model the motion of objects under the influence of gravity. In economics, we can use trinomial standard form to model the behavior of markets and optimize profits.

Real-World Applications

• Physics: modeling motion under gravity.
• Engineering: designing systems and optimizing performance.
• Economics: modeling markets and optimizing profits.

In conclusion, mastering trinomial standard form is an essential skill in algebra, and it requires practice and dedication. By following these five easy steps, we can write trinomials in standard form, factor them, and apply them in real-world applications.

We encourage you to practice writing trinomials in standard form, factoring them, and applying them in real-world scenarios. Share your experiences and examples with us, and let's learn together!