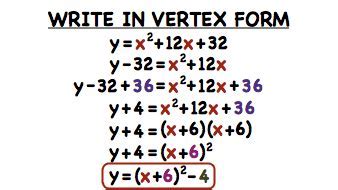Converting standard form to vertex form is an essential skill in algebra, as it allows us to identify the vertex of a parabola, which is crucial in graphing and solving quadratic equations. In this article, we will explore five ways to convert standard form to vertex form, providing you with a comprehensive understanding of this process.
Understanding Standard and Vertex Form
Before we dive into the conversion methods, let's briefly review the standard and vertex forms of a quadratic equation. The standard form of a quadratic equation is:
ax^2 + bx + c = 0
where a, b, and c are constants.
The vertex form of a quadratic equation is:
a(x - h)^2 + k = 0
where (h, k) is the vertex of the parabola.
Method 1: Completing the Square
One of the most common methods to convert standard form to vertex form is by completing the square. This method involves manipulating the equation to create a perfect square trinomial.

For example, let's convert the equation x^2 + 6x + 8 = 0 to vertex form using completing the square.
x^2 + 6x + 8 = 0
We can start by moving the constant term to the right-hand side:
x^2 + 6x = -8
Next, we add (b/2)^2 to both sides, where b is the coefficient of the x term. In this case, b = 6, so we add (6/2)^2 = 9 to both sides:
x^2 + 6x + 9 = -8 + 9
This simplifies to:
(x + 3)^2 = 1
Now, we can rewrite the equation in vertex form:
(x + 3)^2 - 1 = 0
(x - (-3))^2 - 1 = 0
This tells us that the vertex of the parabola is at (-3, -1).
Method 2: Using the Formula
Another method to convert standard form to vertex form is by using the formula:
h = -b/2a k = c - b^2/4a

Using this formula, we can find the vertex of the parabola without having to complete the square.
For example, let's convert the equation x^2 + 4x + 4 = 0 to vertex form using the formula.
h = -b/2a = -4/2(1) = -2
k = c - b^2/4a = 4 - 4^2/4(1) = 4 - 4 = 0
So, the vertex of the parabola is at (-2, 0).
Method 3: Graphing
A third method to convert standard form to vertex form is by graphing the parabola. By graphing the parabola, we can visually identify the vertex and write the equation in vertex form.

For example, let's convert the equation x^2 - 2x - 3 = 0 to vertex form by graphing.
By graphing the parabola, we can see that the vertex is at (1, -4). Therefore, we can write the equation in vertex form:
(x - 1)^2 - 4 = 0
Method 4: Using a Table
A fourth method to convert standard form to vertex form is by using a table. By creating a table of values for the x and y coordinates, we can identify the vertex and write the equation in vertex form.

For example, let's convert the equation x^2 + 2x + 1 = 0 to vertex form using a table.
By examining the table, we can see that the vertex is at (-1, 0). Therefore, we can write the equation in vertex form:
(x + 1)^2 = 0
Method 5: Using Technology
A fifth method to convert standard form to vertex form is by using technology, such as a graphing calculator or computer software.

Using technology, we can quickly and easily graph the parabola and identify the vertex.
For example, let's convert the equation x^2 - 4x + 3 = 0 to vertex form using a graphing calculator.
By graphing the parabola, we can see that the vertex is at (2, -1). Therefore, we can write the equation in vertex form:
(x - 2)^2 - 1 = 0
Conclusion
In conclusion, there are several methods to convert standard form to vertex form, each with its own advantages and disadvantages. Whether you prefer to use completing the square, the formula, graphing, a table, or technology, the key is to find the method that works best for you and to practice, practice, practice!
We hope this article has helped you to better understand the process of converting standard form to vertex form. Remember to take your time, be patient, and don't be afraid to ask for help if you need it.
What's your favorite method for converting standard form to vertex form? Share your thoughts and experiences in the comments below!
What is the difference between standard form and vertex form?
+The standard form of a quadratic equation is ax^2 + bx + c = 0, while the vertex form is a(x - h)^2 + k = 0. The vertex form is useful for identifying the vertex of a parabola.
How do I know which method to use to convert standard form to vertex form?
+The choice of method depends on your personal preference and the specific problem. Completing the square is a good method to use when the coefficient of the x^2 term is 1. The formula is useful when you need to find the vertex quickly. Graphing and using a table are good methods to use when you need to visualize the parabola. Technology is useful when you need to graph the parabola quickly.
Can I use more than one method to convert standard form to vertex form?
+Yes, you can use more than one method to convert standard form to vertex form. In fact, using multiple methods can help you to check your work and ensure that you have the correct answer.