5 Steps To Simplify Radical Expressions

Quick Links :

Radical expressions can be intimidating, especially when they involve complex equations and formulas. However, with the right approach, simplifying radical expressions can become a manageable task. In this article, we will explore the 5 essential steps to simplify radical expressions, making it easier for you to tackle even the most challenging problems.

Simplifying radical expressions is an essential skill in mathematics, particularly in algebra and geometry. It allows you to manipulate equations, solve problems, and visualize mathematical concepts more effectively. By mastering these 5 steps, you'll become more confident in your ability to work with radical expressions and tackle more advanced math concepts.

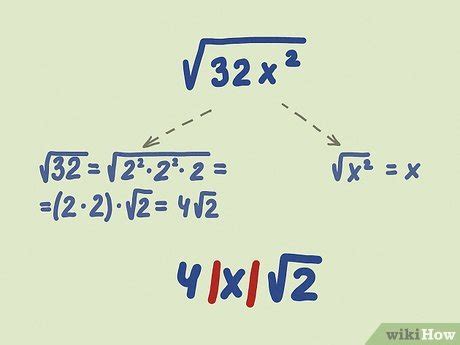
Step 1: Factor Out Perfect Squares

The first step in simplifying radical expressions is to factor out perfect squares. A perfect square is a number that can be expressed as the square of an integer, such as 16 (4^2) or 25 (5^2). When you have a perfect square inside a radical expression, you can simplify it by factoring it out.

For example, consider the expression √(16x^2). Since 16 is a perfect square (4^2), you can factor it out of the radical expression:

√(16x^2) = √(4^2x^2) = 4x√(x^2)

By factoring out the perfect square, you've simplified the expression and made it easier to work with.

Key Takeaway: Factor out perfect squares to simplify radical expressions

Step 2: Simplify Radicals with Variables

When working with radical expressions that involve variables, it's essential to simplify the radicals by combining like terms. Consider the expression √(x^2 + 4x + 4). To simplify this expression, you can combine the like terms inside the radical:

√(x^2 + 4x + 4) = √((x+2)^2) = x+2

By combining the like terms, you've simplified the expression and made it easier to work with.

Key Takeaway: Combine like terms to simplify radical expressions with variables

Step 3: Rationalize the Denominator

When working with radical expressions, it's often necessary to rationalize the denominator. Rationalizing the denominator involves multiplying the numerator and denominator by a radical expression that eliminates the radical in the denominator.

For example, consider the expression 1/√2. To rationalize the denominator, you can multiply the numerator and denominator by √2:

1/√2 = (1 × √2) / (√2 × √2) = √2 / 2

By rationalizing the denominator, you've simplified the expression and made it easier to work with.

Key Takeaway: Rationalize the denominator to simplify radical expressions

Step 4: Simplify Radicals with Coefficients

When working with radical expressions that involve coefficients, it's essential to simplify the radicals by combining like terms. Consider the expression 2√(x^2 + 4x + 4). To simplify this expression, you can combine the like terms inside the radical:

2√(x^2 + 4x + 4) = 2√((x+2)^2) = 2(x+2)

By combining the like terms, you've simplified the expression and made it easier to work with.

Key Takeaway: Combine like terms to simplify radical expressions with coefficients

Step 5: Check for Any Remaining Simplifications

After simplifying the radical expression using the previous steps, it's essential to check for any remaining simplifications. Consider the expression 2(x+2). While this expression is simplified, you may be able to simplify it further by combining like terms or factoring out perfect squares.

For example, if you have the expression 2(x+2) + 4, you can combine the like terms:

2(x+2) + 4 = 2x + 4 + 4 = 2x + 8

By checking for any remaining simplifications, you've ensured that the expression is fully simplified.

Key Takeaway: Check for any remaining simplifications to ensure the expression is fully simplified

In conclusion, simplifying radical expressions requires a combination of factoring out perfect squares, simplifying radicals with variables, rationalizing the denominator, simplifying radicals with coefficients, and checking for any remaining simplifications. By mastering these 5 steps, you'll become more confident in your ability to work with radical expressions and tackle more advanced math concepts.

We hope this article has helped you understand the 5 essential steps to simplify radical expressions. If you have any questions or need further clarification, please don't hesitate to ask.