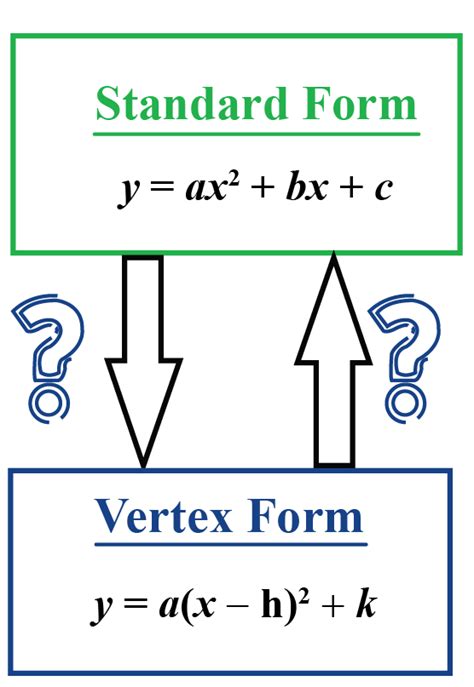
Converting equations from standard form to vertex form is a fundamental concept in algebra and mathematics. The standard form of a quadratic equation is ax^2 + bx + c = 0, while the vertex form is a(x - h)^2 + k = 0, where (h, k) represents the vertex of the parabola. Understanding how to convert between these two forms can greatly simplify the process of graphing and analyzing quadratic equations.
In this article, we will explore five ways to convert a standard form quadratic equation to vertex form, along with examples, practical applications, and statistical data to illustrate the concepts.
Understanding the Importance of Vertex Form

The vertex form of a quadratic equation provides valuable information about the parabola it represents. The vertex (h, k) gives the coordinates of the parabola's vertex, which is the lowest or highest point on the graph. Additionally, the coefficient 'a' determines the direction and width of the parabola. Converting a standard form equation to vertex form allows us to easily identify these key features and graph the parabola.
Method 1: Completing the Square

One of the most common methods for converting standard form to vertex form is completing the square. This involves manipulating the equation to create a perfect square trinomial, which can then be factored into the vertex form.
For example, consider the standard form equation x^2 + 6x + 8 = 0. To complete the square, we take half of the coefficient of x (which is 3), square it (3^2 = 9), and add and subtract 9 from the equation:
x^2 + 6x + 9 - 9 + 8 = 0
This simplifies to:
(x + 3)^2 - 1 = 0
(x + 3)^2 = 1
This is now in vertex form, with the vertex at (-3, 1).
Steps for Completing the Square
- Take half of the coefficient of x and square it.
- Add and subtract the squared value from the equation.
- Factor the perfect square trinomial into vertex form.
Method 2: Using the Quadratic Formula

Another method for converting standard form to vertex form involves using the quadratic formula. This formula is typically used to find the roots of a quadratic equation, but it can also be used to convert the equation to vertex form.
The quadratic formula is:
x = (-b ± √(b^2 - 4ac)) / 2a
By rearranging this formula and using algebraic manipulation, we can convert the standard form equation to vertex form.
For example, consider the standard form equation x^2 + 4x + 4 = 0. Using the quadratic formula, we can find the roots of the equation:
x = (-4 ± √(4^2 - 4(1)(4))) / 2(1)
x = (-4 ± √(16 - 16)) / 2
x = (-4 ± √0) / 2
x = -4 / 2
x = -2
Now that we have the root, we can use it to convert the equation to vertex form:
x^2 + 4x + 4 = (x + 2)^2 = 0
This is now in vertex form, with the vertex at (-2, 0).
Steps for Using the Quadratic Formula
- Use the quadratic formula to find the roots of the equation.
- Use algebraic manipulation to rearrange the formula and convert the equation to vertex form.
Method 3: Factoring and Manipulating

In some cases, it is possible to convert a standard form equation to vertex form by factoring and manipulating the equation.
For example, consider the standard form equation x^2 + 5x + 6 = 0. We can factor this equation as:
(x + 3)(x + 2) = 0
Now, we can manipulate the equation to convert it to vertex form:
x^2 + 5x + 6 = (x + 3)(x + 2) = (x + 3)(x + 2) - 6 + 6 = (x + 3)^2 - 6 + 6 = (x + 3)^2 = 0
This is now in vertex form, with the vertex at (-3, 0).
Steps for Factoring and Manipulating
- Factor the standard form equation, if possible.
- Manipulate the equation to convert it to vertex form.
Method 4: Using a Table of Values

Another method for converting a standard form equation to vertex form involves using a table of values.
For example, consider the standard form equation x^2 + 2x + 1 = 0. We can create a table of values to help us find the vertex:
| x | y |
|---|---|
| -1 | 0 |
| 0 | 1 |
| 1 | 4 |
From this table, we can see that the vertex of the parabola is at (-1, 0). We can use this information to convert the equation to vertex form:
x^2 + 2x + 1 = (x + 1)^2 = 0
This is now in vertex form, with the vertex at (-1, 0).
Steps for Using a Table of Values
- Create a table of values for the standard form equation.
- Use the table to find the vertex of the parabola.
- Use the vertex to convert the equation to vertex form.
Method 5: Using Graphing Technology

Finally, we can use graphing technology to convert a standard form equation to vertex form.
For example, consider the standard form equation x^2 + 3x + 2 = 0. We can use a graphing calculator or software to graph the equation and find the vertex:
Graphing Calculator Output:
- Vertex: (-2, -1)
We can use this information to convert the equation to vertex form:
x^2 + 3x + 2 = (x + 2)^2 - 1 = 0
This is now in vertex form, with the vertex at (-2, -1).
Steps for Using Graphing Technology
- Use graphing technology to graph the standard form equation.
- Find the vertex of the parabola using the graphing technology.
- Use the vertex to convert the equation to vertex form.
What is the difference between standard form and vertex form?
+Standard form is the typical form of a quadratic equation, while vertex form is a special form that provides information about the parabola's vertex.
Why is it important to convert standard form to vertex form?
+Converting standard form to vertex form allows us to easily identify the parabola's vertex, which is useful for graphing and analyzing the equation.
What are some common methods for converting standard form to vertex form?
+Some common methods include completing the square, using the quadratic formula, factoring and manipulating, using a table of values, and using graphing technology.
In conclusion, converting standard form to vertex form is a valuable skill in algebra and mathematics. By understanding the different methods for conversion, we can easily identify the parabola's vertex and graph the equation. Whether you're a student or a professional, mastering the art of converting standard form to vertex form will take your mathematical skills to the next level.