Find Standard Form Of A Parabola In Simple Steps

Quick Links :

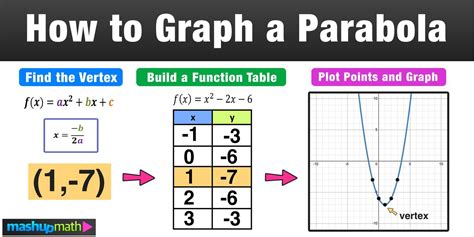
The standard form of a parabola is a fundamental concept in algebra and geometry, and it's essential to understand how to find it in order to analyze and solve problems related to quadratic equations and functions. In this article, we'll break down the process of finding the standard form of a parabola into simple steps, making it easy for you to grasp and apply this concept.

Understanding the Standard Form of a Parabola

The standard form of a parabola is a mathematical representation that provides valuable information about the parabola's shape, size, and orientation. The standard form of a parabola is given by the equation:

y = a(x - h)^2 + k

where (h, k) is the vertex of the parabola, and 'a' is a coefficient that determines the parabola's width and direction.

Step 1: Identify the Vertex (h, k)

The vertex of a parabola is the lowest or highest point on the curve, depending on the parabola's orientation. To find the vertex, you can use the following methods:

• If you have the equation of the parabola in the form y = ax^2 + bx + c, you can complete the square to find the vertex.
• If you have the graph of the parabola, you can identify the vertex by looking for the lowest or highest point on the curve.

Completing the Square to Find the Vertex

Completing the square is a powerful technique used to rewrite a quadratic equation in the standard form of a parabola. Here's how to do it:

• Start with the equation y = ax^2 + bx + c
• Move the constant term to the right-hand side: y - c = ax^2 + bx
• Add and subtract (b/2)^2 to the right-hand side: y - c = ax^2 + bx + (b/2)^2 - (b/2)^2
• Factor the left-hand side: y - c = a(x + b/2)^2 - (b/2)^2
• Simplify the equation: y = a(x + b/2)^2 - (b/2)^2 + c

Step 2: Determine the Coefficient 'a'

The coefficient 'a' determines the parabola's width and direction. If 'a' is positive, the parabola opens upward; if 'a' is negative, the parabola opens downward. To find 'a', you can use the following methods:

• If you have the equation of the parabola in the form y = ax^2 + bx + c, 'a' is the coefficient of the x^2 term.
• If you have the graph of the parabola, you can estimate 'a' by looking at the parabola's width and direction.

Putting it All Together

Now that you have the vertex (h, k) and the coefficient 'a', you can write the standard form of the parabola:

y = a(x - h)^2 + k

This equation provides valuable information about the parabola's shape, size, and orientation, making it easier to analyze and solve problems related to quadratic equations and functions.

Example: Finding the Standard Form of a Parabola

Suppose we have the equation y = x^2 + 4x + 3. To find the standard form of the parabola, we need to complete the square:

y = x^2 + 4x + 3 y - 3 = x^2 + 4x y - 3 = x^2 + 4x + 4 - 4 y - 3 = (x + 2)^2 - 4 y = (x + 2)^2 - 4 + 3 y = (x + 2)^2 - 1

The standard form of the parabola is y = (x + 2)^2 - 1, where (h, k) = (-2, -1) and 'a' = 1.

Conclusion

Finding the standard form of a parabola is a crucial step in analyzing and solving problems related to quadratic equations and functions. By following these simple steps, you can easily find the standard form of a parabola and gain valuable insights into its shape, size, and orientation. Remember to practice and apply this concept to different problems to become more proficient in finding the standard form of a parabola.