5 Ways To Convert Standard Form To General Form

Quick Links :

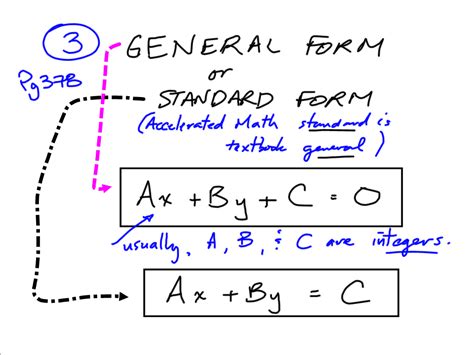
Converting standard form to general form is an essential skill in algebra and mathematics. The standard form of a linear equation is ax + by = c, where a, b, and c are constants. However, in many situations, it is more convenient to work with the general form of a linear equation, which is ax + by + cz = d. In this article, we will explore five ways to convert standard form to general form.

Understanding the Importance of Converting Standard Form to General Form

Converting standard form to general form is crucial in various mathematical operations, such as solving systems of linear equations, graphing linear equations, and performing linear transformations. The general form provides more flexibility and allows for easier manipulation of the equation. Moreover, many mathematical software and calculators use the general form as the default input format.

Method 1: Adding a Zero Term

One simple way to convert standard form to general form is to add a zero term to the equation. This method involves adding a term with a coefficient of zero to the equation, effectively converting it to the general form.

Example: Convert the equation 2x + 3y = 4 to general form.

Solution: Add a zero term to the equation: 2x + 3y + 0z = 4.

Advantages and Disadvantages of Method 1

Advantages:

• Simple and easy to implement
• Does not alter the original equation

Disadvantages:

• May not be suitable for equations with multiple variables
• Does not provide any additional information or insight

Method 2: Rearranging Terms

Another way to convert standard form to general form is to rearrange the terms of the equation. This method involves rearranging the terms to match the general form format.

Example: Convert the equation x + 2y = 3 to general form.

Solution: Rearrange the terms: x + 0z + 2y = 3.

Advantages and Disadvantages of Method 2

Advantages:

• Allows for greater flexibility in rearranging terms
• Can be used for equations with multiple variables

Disadvantages:

• May require additional calculations or manipulations
• May not be as straightforward as Method 1

Method 3: Using the Distributive Property

The distributive property can be used to convert standard form to general form. This method involves using the distributive property to expand and rearrange the terms of the equation.

Example: Convert the equation 2(x + y) = 4 to general form.

Solution: Use the distributive property: 2x + 2y = 4.

Advantages and Disadvantages of Method 3

Advantages:

• Allows for greater flexibility in rearranging terms
• Can be used for equations with multiple variables

Disadvantages:

• May require additional calculations or manipulations
• May not be as straightforward as Method 1

Method 4: Using Algebraic Manipulations

Algebraic manipulations, such as multiplying or dividing both sides of the equation by a constant, can be used to convert standard form to general form.

Example: Convert the equation x + 2y = 3 to general form.

Solution: Multiply both sides of the equation by 2: 2x + 4y = 6.

Advantages and Disadvantages of Method 4

Advantages:

• Allows for greater flexibility in rearranging terms
• Can be used for equations with multiple variables

Disadvantages:

• May require additional calculations or manipulations
• May alter the original equation

Method 5: Using Matrix Operations

Matrix operations, such as matrix multiplication or matrix addition, can be used to convert standard form to general form.

Example: Convert the equation x + 2y = 3 to general form using matrix operations.

Solution: Represent the equation as a matrix equation: [1 2] [x y] = [3].

Advantages and Disadvantages of Method 5

Advantages:

• Allows for greater flexibility in rearranging terms
• Can be used for equations with multiple variables

Disadvantages:

• May require additional calculations or manipulations
• May not be as straightforward as other methods

In conclusion, converting standard form to general form is an essential skill in algebra and mathematics. The five methods presented in this article provide different approaches to achieving this conversion. Each method has its advantages and disadvantages, and the choice of method depends on the specific equation and the desired outcome.

We encourage you to try out these methods and practice converting standard form to general form. Share your thoughts and questions in the comments section below.