Sphere Equation In Standard Form Explained Simply

Quick Links :

Understanding the equation of a sphere is a fundamental concept in mathematics, particularly in geometry and calculus. A sphere is a three-dimensional shape that is perfectly symmetrical about its center, and its equation is essential in various fields, including physics, engineering, and computer graphics. In this article, we will delve into the sphere equation in standard form, explaining it in a simple and comprehensive manner.

What is a Sphere?

A sphere is a three-dimensional geometric shape that is perfectly symmetrical about its center. It is defined as the set of all points in space that are equidistant from a fixed central point called the center. The distance from the center to any point on the sphere is called the radius. A sphere has several important properties, including its center, radius, diameter, circumference, and surface area.

The Equation of a Sphere

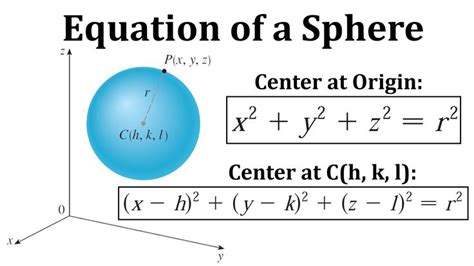
The equation of a sphere in standard form is given by:

(x - h)^2 + (y - k)^2 + (z - l)^2 = r^2

where:

• (x, y, z) are the coordinates of any point on the sphere
• (h, k, l) are the coordinates of the center of the sphere
• r is the radius of the sphere

This equation represents the set of all points in space that are equidistant from the center of the sphere. The distance from the center to any point on the sphere is given by the radius, which is a fixed value.

Derivation of the Equation

The equation of a sphere can be derived using the Pythagorean theorem in three dimensions. Consider a point P(x, y, z) on the surface of the sphere, and let C(h, k, l) be the center of the sphere. The distance from the center to the point P is given by the radius r.

Using the Pythagorean theorem, we can write:

(x - h)^2 + (y - k)^2 + (z - l)^2 = r^2

This equation represents the set of all points in space that are equidistant from the center of the sphere.

Understanding the Equation

The equation of a sphere in standard form is a powerful tool for understanding the properties and behavior of spheres in various fields. Here are some key aspects of the equation:

• The equation represents the set of all points in space that are equidistant from the center of the sphere.
• The distance from the center to any point on the sphere is given by the radius.
• The equation is symmetrical about the center of the sphere.
• The equation can be used to find the coordinates of points on the surface of the sphere.

Applications of the Equation

The equation of a sphere has numerous applications in various fields, including:

• Physics: The equation is used to model the motion of objects in three-dimensional space, such as the trajectory of a projectile or the orbit of a planet.
• Engineering: The equation is used to design and analyze systems that involve spherical shapes, such as pipelines, tanks, and spherical bearings.
• Computer Graphics: The equation is used to create three-dimensional models of spheres and other shapes, and to perform calculations involving these shapes.

Examples and Exercises

Here are some examples and exercises to help you understand the equation of a sphere:

• Find the equation of a sphere with center (2, 3, 4) and radius 5.
• Find the coordinates of the points on the surface of a sphere with center (0, 0, 0) and radius 3.
• Use the equation of a sphere to find the distance from the center to a point on the surface.

Conclusion

The equation of a sphere in standard form is a fundamental concept in mathematics and has numerous applications in various fields. By understanding the equation and its properties, you can solve problems involving spherical shapes and analyze systems that involve these shapes. We hope this article has provided a comprehensive and accessible explanation of the sphere equation.