The sphere is one of the most fundamental shapes in geometry, and understanding its standard form is crucial for various mathematical and real-world applications. From architecture to engineering, the sphere plays a significant role in designing and constructing curved surfaces, modeling celestial bodies, and optimizing systems. In this article, we will delve into the standard form of spheres, exploring their properties, equations, and applications.
The Importance of Spheres in Geometry

Spheres are three-dimensional shapes that are perfectly symmetrical about their centers. They have no edges or corners, and every point on the surface is equidistant from the center. This unique property makes spheres essential in geometry, as they can be used to model various real-world objects, such as planets, balls, and even the Earth itself.
Properties of Spheres
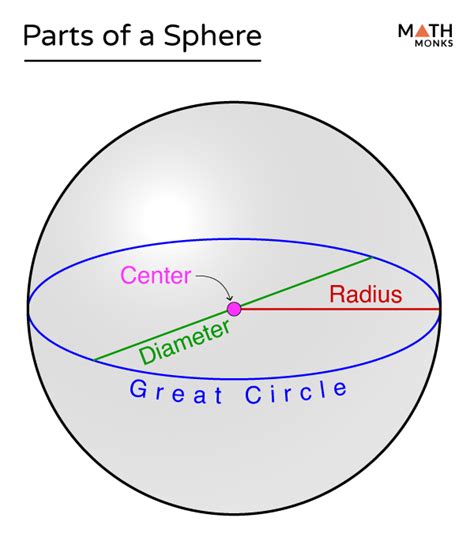
A sphere is defined by its center, radius, and diameter. The center is the point that is equidistant from all points on the surface, while the radius is the distance from the center to any point on the surface. The diameter is twice the radius and passes through the center. Spheres also have a surface area and volume, which can be calculated using specific formulas.
Standard Form of a Sphere

The standard form of a sphere is given by the equation:
(x - h)^2 + (y - k)^2 + (z - l)^2 = r^2
where (h, k, l) is the center of the sphere, and r is the radius. This equation represents a sphere with its center at (h, k, l) and a radius of r.
Equations of Spheres
There are several types of equations that can represent a sphere, including:
- The standard form equation: (x - h)^2 + (y - k)^2 + (z - l)^2 = r^2
- The parametric equation: x = h + r sin(φ) cos(θ), y = k + r sin(φ) sin(θ), z = l + r cos(φ)
- The implicit equation: x^2 + y^2 + z^2 - 2hx - 2ky - 2lz + h^2 + k^2 + l^2 - r^2 = 0
These equations can be used to represent different types of spheres, including ones with varying radii, centers, and orientations.
Applications of Spheres in Real-World Problems

Spheres have numerous applications in real-world problems, including:
- Architecture: Spheres are used in designing curved surfaces, such as domes and arches.
- Engineering: Spheres are used in modeling celestial bodies, optimizing systems, and designing curved pipes and tubes.
- Physics: Spheres are used in modeling the motion of objects, such as projectiles and planets.
- Computer Graphics: Spheres are used in creating 3D models and animations.
Practical Examples of Spheres in Real-World Problems
Some practical examples of spheres in real-world problems include:
- The design of the dome of the United States Capitol Building, which is a perfect sphere.
- The modeling of the Earth's orbit around the Sun, which is an ellipse that can be approximated by a sphere.
- The design of curved pipes and tubes in engineering systems, which often use spherical shapes to minimize friction and maximize flow.
Conclusion
In conclusion, spheres are a fundamental shape in geometry, and understanding their standard form is crucial for various mathematical and real-world applications. By recognizing the properties, equations, and applications of spheres, we can better appreciate the importance of this shape in our everyday lives. Whether it's designing curved surfaces, modeling celestial bodies, or optimizing systems, the sphere plays a significant role in shaping our world.
What is the standard form of a sphere?
+The standard form of a sphere is given by the equation: (x - h)^2 + (y - k)^2 + (z - l)^2 = r^2, where (h, k, l) is the center of the sphere, and r is the radius.
What are some applications of spheres in real-world problems?
+Spheres have numerous applications in real-world problems, including architecture, engineering, physics, and computer graphics.
What is the surface area of a sphere?
+The surface area of a sphere is given by the formula: A = 4πr^2, where r is the radius of the sphere.