Easy Ways To Find Square Root Of 48 Radical Form

Quick Links :

Finding the square root of 48 in radical form may seem daunting, but it's actually a straightforward process. In this article, we'll break down the steps to simplify the square root of 48 and provide you with a clear understanding of the concept.

Understanding Square Roots

Before we dive into finding the square root of 48, let's quickly review what a square root is. A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4, because 4 multiplied by 4 equals 16.

Why Radical Form?

Radical form is a way of expressing square roots using the radical symbol (√). It's a more concise and elegant way to represent square roots, especially when dealing with complex numbers or algebraic expressions.

Breaking Down the Square Root of 48

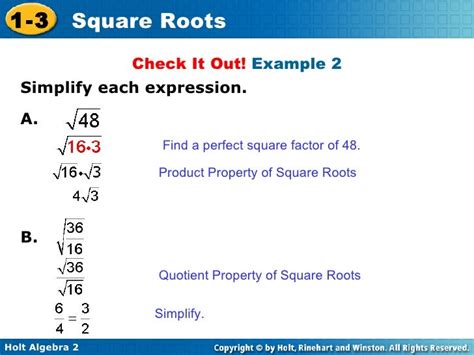
To find the square root of 48 in radical form, we need to factor 48 into its prime factors. The prime factorization of 48 is:

48 = 2 × 2 × 2 × 2 × 3

Now, let's look for pairs of identical factors:

(2 × 2) × (2 × 2) × 3

We can rewrite this as:

(2^2) × (2^2) × 3

Taking the square root of both sides, we get:

√48 = √((2^2) × (2^2) × 3)

Using the property of square roots that allows us to split the radical into separate factors, we can rewrite this as:

√48 = 2 × 2 × √3

Simplifying further, we get:

√48 = 4√3

Alternative Methods

While the method above is the most straightforward way to find the square root of 48 in radical form, there are alternative methods you can use.

• Using a calculator: You can use a calculator to find the square root of 48, which will give you an approximate value. However, this method won't give you the radical form.
• Factoring out perfect squares: You can factor out perfect squares from the radicand (the number inside the square root). For example, you can rewrite √48 as √(16 × 3), which simplifies to 4√3.

Practical Applications

Finding the square root of 48 in radical form has several practical applications in mathematics, physics, and engineering. For example:

• Quadratic equations: When solving quadratic equations, you often need to find the square root of a number. Knowing how to simplify square roots in radical form can make the process easier.
• Geometry: In geometry, you may need to find the length of a side of a triangle or the area of a shape. Simplifying square roots in radical form can help you solve these problems more efficiently.
• Physics: In physics, you may need to calculate distances, velocities, or accelerations. Simplifying square roots in radical form can help you simplify complex equations.

Conclusion

Finding the square root of 48 in radical form is a straightforward process that requires factoring the number into its prime factors and simplifying the radical expression. By understanding the concept of square roots and radical form, you can apply this knowledge to solve problems in mathematics, physics, and engineering.

We hope this article has helped you understand how to find the square root of 48 in radical form. If you have any questions or need further clarification, please don't hesitate to ask.

Now it's your turn! Share your thoughts on finding square roots in radical form. Do you have any favorite methods or tips? Share your experiences in the comments below.