Calculate Square Root Of 42 In Radical Form

Quick Links :

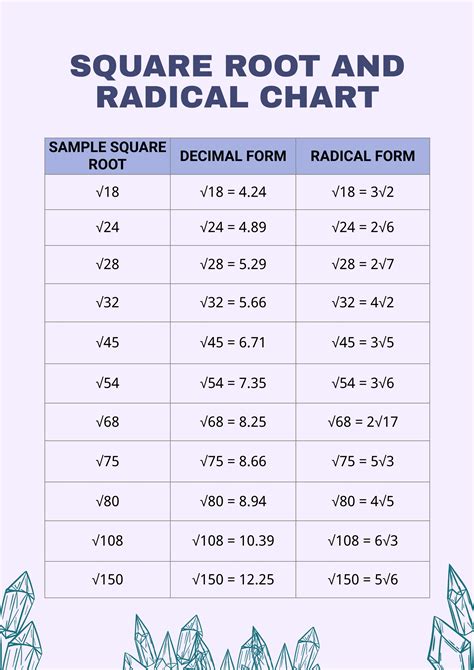
The square root of 42 is a mathematical expression that can be simplified using radical form. Radical form is a way of expressing a number using roots, such as square roots, cube roots, and so on.

To calculate the square root of 42 in radical form, we need to find a number that, when multiplied by itself, gives us 42. Since 42 is not a perfect square, we cannot simplify it to a whole number. However, we can simplify it to a radical expression.

First, let's factorize 42:

42 = 2 × 3 × 7

Now, let's take the square root of 42:

√42 = √(2 × 3 × 7)

We can simplify this expression by taking the square root of each factor:

√42 = √2 × √3 × √7

Therefore, the square root of 42 in radical form is:

√42 = √2 × √3 × √7

Or, in a more simplified form:

√42 = √(6 × 7)

√42 = √6 × √7

What is Radical Form?

Radical form is a way of expressing a number using roots, such as square roots, cube roots, and so on. It is a mathematical notation that uses a symbol, such as √, to indicate the root of a number. Radical form is used to simplify complex mathematical expressions and to make them easier to work with.

Why is Radical Form Important?

Radical form is important because it allows us to simplify complex mathematical expressions and to make them easier to work with. It is used in a variety of mathematical operations, such as algebra, geometry, and calculus. Radical form is also used in science and engineering to describe physical phenomena, such as the motion of objects and the behavior of electrical circuits.

How to Simplify Radical Expressions

Simplifying radical expressions involves finding the square root or other roots of a number and expressing it in a simpler form. Here are some steps to simplify radical expressions:

1. Factorize the number: Factorize the number inside the radical sign into its prime factors.
2. Take the square root of each factor: Take the square root of each factor and simplify the expression.
3. Combine like terms: Combine like terms and simplify the expression further.

Example: Simplifying a Radical Expression

Let's simplify the radical expression:

√48

First, factorize 48:

48 = 2 × 2 × 2 × 2 × 3

Now, take the square root of each factor:

√48 = √(2 × 2 × 2 × 2 × 3)

Simplify the expression:

√48 = √(2^2 × 2^2 × 3)

√48 = 4√3

Therefore, the simplified radical form of √48 is 4√3.

Applications of Radical Form

Radical form has a variety of applications in mathematics, science, and engineering. Here are some examples:

1. Algebra: Radical form is used to simplify algebraic expressions and to solve equations.
2. Geometry: Radical form is used to describe geometric shapes, such as triangles and circles.
3. Calculus: Radical form is used to describe rates of change and to solve optimization problems.
4. Science: Radical form is used to describe physical phenomena, such as the motion of objects and the behavior of electrical circuits.
5. Engineering: Radical form is used to design and optimize systems, such as electronic circuits and mechanical systems.

Conclusion

In conclusion, the square root of 42 in radical form is √2 × √3 × √7. Radical form is a powerful mathematical notation that is used to simplify complex expressions and to make them easier to work with. It has a variety of applications in mathematics, science, and engineering.

Call to Action

We hope this article has helped you to understand the concept of radical form and how to simplify radical expressions. Do you have any questions or comments about radical form? Share your thoughts with us in the comments section below.