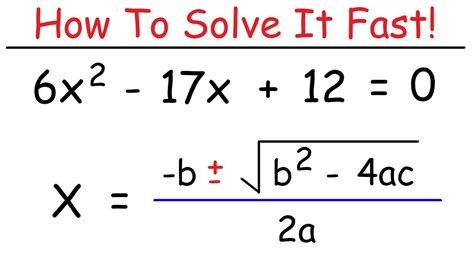Solve Quadratics In 2 Easy Steps

Quick Links :

Quadratic equations are a fundamental concept in algebra, and being able to solve them is an essential skill for anyone studying mathematics or science. The good news is that solving quadratics can be broken down into two easy steps, making it accessible to anyone with a basic understanding of algebra.

Quadratic equations are equations of the form ax^2 + bx + c = 0, where a, b, and c are constants. They can be used to model a wide range of real-world situations, from the trajectory of a projectile to the growth of a population. However, solving quadratics can seem daunting, especially for those who are new to algebra. But with the right approach, anyone can learn to solve quadratics with ease.

Step 1: Factor the Quadratic

The first step in solving a quadratic equation is to try and factor it. Factoring involves expressing the quadratic as a product of two binomials. This can be done by looking for two numbers whose product is equal to the constant term (c) and whose sum is equal to the coefficient of the linear term (b). These numbers can then be used to rewrite the quadratic as a product of two binomials.

For example, consider the quadratic equation x^2 + 5x + 6 = 0. We can factor this by looking for two numbers whose product is 6 and whose sum is 5. These numbers are 2 and 3, so we can rewrite the quadratic as (x + 2)(x + 3) = 0.

Factoring Tips

• Always look for the greatest common factor (GCF) of the terms first.
• Use the product-sum method to find the factors.
• Check your factors by multiplying them out to ensure they equal the original quadratic.

Step 2: Set Each Factor Equal to Zero

Once you have factored the quadratic, the next step is to set each factor equal to zero and solve for x. This is based on the zero product property, which states that if the product of two numbers is zero, then at least one of the numbers must be zero.

Using the example from earlier, we can set each factor equal to zero and solve for x:

(x + 2) = 0 --> x = -2 (x + 3) = 0 --> x = -3

Therefore, the solutions to the quadratic equation x^2 + 5x + 6 = 0 are x = -2 and x = -3.

Solving Quadratics with the Quadratic Formula

While factoring is a great way to solve quadratics, it's not always possible. In these cases, you can use the quadratic formula:

x = (-b ± √(b^2 - 4ac)) / 2a

This formula will give you the solutions to the quadratic equation, but it's often more complicated than factoring.

Real-World Applications of Quadratics

Quadratic equations have a wide range of real-world applications, from physics and engineering to economics and computer science. Here are a few examples:

• Projectile motion: Quadratics can be used to model the trajectory of a projectile, such as a ball or a rocket.
• Electronic circuits: Quadratics can be used to analyze the behavior of electronic circuits.
• Population growth: Quadratics can be used to model the growth of a population over time.

Conclusion

Solving quadratics may seem daunting, but it can be broken down into two easy steps: factoring and setting each factor equal to zero. By mastering these steps, you can solve quadratics with ease and tackle a wide range of real-world problems. Whether you're a student or a professional, being able to solve quadratics is an essential skill that will serve you well in your mathematical and scientific endeavors.

We hope this article has been helpful in explaining the steps to solve quadratics. Do you have any questions or comments about solving quadratics? Share them with us in the comments below!