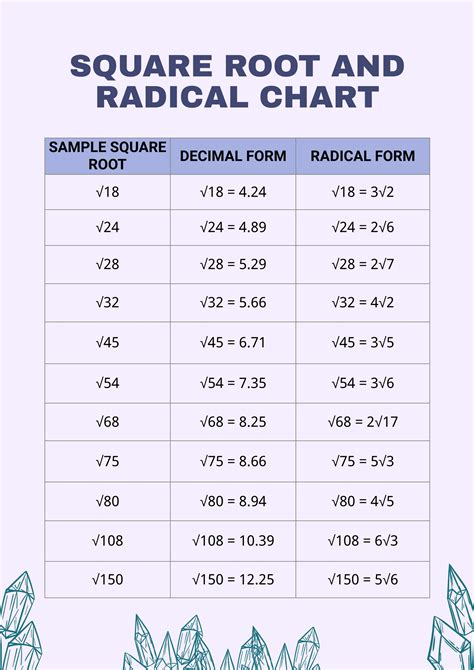
The square root of 24 is a fundamental concept in mathematics, and understanding its radical form is essential for various mathematical operations. In this article, we will delve into the world of square roots, explore the radical form of the square root of 24, and provide a comprehensive explanation of its significance.
What is a Square Root?

A square root of a number is a value that, when multiplied by itself, gives the original number. It is denoted by the symbol √ and is used to find the number that, when raised to the power of 1/2, equals the given value. For example, the square root of 16 is 4, because 4 multiplied by 4 equals 16.
Radical Form: A Deeper Understanding

In mathematics, the radical form is a way of expressing square roots and other roots in a simplified manner. It involves breaking down a number into its prime factors and then simplifying the expression using the properties of radicals. The radical form of a number can be used to perform various mathematical operations, such as addition, subtraction, multiplication, and division.
The Square Root of 24 in Radical Form

To find the square root of 24 in radical form, we need to break down 24 into its prime factors. The prime factorization of 24 is:
24 = 2 × 2 × 2 × 3
Now, we can simplify the expression using the properties of radicals:
√24 = √(2 × 2 × 2 × 3) = √(2^2 × 2 × 3) = 2√(2 × 3) = 2√6
Therefore, the square root of 24 in radical form is 2√6.
Why is the Radical Form Important?

The radical form of the square root of 24 is essential in various mathematical operations, such as:
- Simplifying expressions: The radical form can be used to simplify complex expressions involving square roots.
- Solving equations: The radical form can be used to solve equations involving square roots.
- Finding roots: The radical form can be used to find the roots of quadratic equations.
In addition, the radical form is used in various real-world applications, such as:
- Physics: The radical form is used to describe the motion of objects in physics.
- Engineering: The radical form is used to design and optimize systems in engineering.
- Computer Science: The radical form is used in algorithms and data structures in computer science.
Common Mistakes to Avoid

When working with the square root of 24 in radical form, there are several common mistakes to avoid:
- Simplifying the expression incorrectly: Make sure to simplify the expression using the properties of radicals.
- Forgetting to include the radical symbol: Make sure to include the radical symbol (√) when expressing the square root of 24 in radical form.
- Confusing the radical form with other forms: Make sure to distinguish the radical form from other forms, such as the decimal form or the fraction form.
Conclusion: A Recap of the Square Root of 24 in Radical Form

In conclusion, the square root of 24 in radical form is an essential concept in mathematics, and understanding its significance is crucial for various mathematical operations. By breaking down 24 into its prime factors and simplifying the expression using the properties of radicals, we can express the square root of 24 in radical form as 2√6. Remember to avoid common mistakes and use the radical form correctly in your mathematical calculations.
We hope this article has provided you with a comprehensive understanding of the square root of 24 in radical form. If you have any questions or need further clarification, please don't hesitate to ask. Share your thoughts and comments below, and don't forget to share this article with your friends and colleagues.
What is the square root of 24 in radical form?
+The square root of 24 in radical form is 2√6.
Why is the radical form important?
+The radical form is important because it is used to simplify complex expressions, solve equations, and find roots in various mathematical operations.
What are some common mistakes to avoid when working with the square root of 24 in radical form?
+Some common mistakes to avoid include simplifying the expression incorrectly, forgetting to include the radical symbol, and confusing the radical form with other forms.