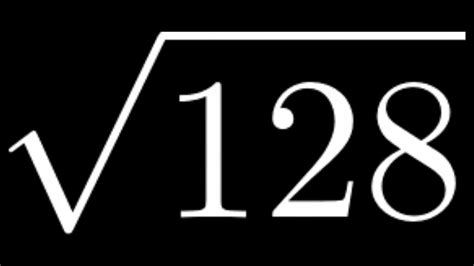Simplify The Square Root Of 128

Quick Links :

The square root of 128 can be simplified by factoring out the largest perfect square from the number.

√128 = √(64 × 2)

Since 64 is a perfect square (8²), we can rewrite the expression as:

√128 = √(8² × 2)

= 8√2

So, the simplified square root of 128 is 8√2.

Here's an image to illustrate the concept:

Now, let's explore some other aspects of simplifying square roots.

What is a Square Root?

A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4, because 4 × 4 = 16.

How to Simplify Square Roots

To simplify a square root, we need to find the largest perfect square that divides the number. We can do this by factoring the number into its prime factors and then grouping the factors into pairs.

For example, let's simplify the square root of 200:

√200 = √(100 × 2)

= √(10² × 2)

= 10√2

So, the simplified square root of 200 is 10√2.

Here's another example:

√450 = √(225 × 2)

= √(15² × 2)

= 15√2

So, the simplified square root of 450 is 15√2.

Types of Square Roots

There are two types of square roots: rational and irrational.

Rational square roots are those that can be expressed as a fraction of two integers. For example, the square root of 16 is a rational square root because it can be expressed as 4/1.

Irrational square roots are those that cannot be expressed as a fraction of two integers. For example, the square root of 2 is an irrational square root because it cannot be expressed as a simple fraction.

Here's an image to illustrate the concept:

Why Simplify Square Roots?

Simplifying square roots is important in mathematics and science because it allows us to work with numbers more easily. Simplified square roots can be used to solve equations, calculate distances, and perform other mathematical operations.

In addition, simplifying square roots can help us to identify patterns and relationships between numbers. For example, the simplified square root of 128 is 8√2, which shows that 128 is related to the perfect square of 64.

Real-World Applications of Simplifying Square Roots

Simplifying square roots has many real-world applications in fields such as physics, engineering, and finance. Here are a few examples:

• In physics, simplifying square roots is used to calculate distances and velocities. For example, the distance between two objects can be calculated using the formula √(x² + y²).
• In engineering, simplifying square roots is used to design buildings and bridges. For example, the length of a bridge can be calculated using the formula √(span² + height²).
• In finance, simplifying square roots is used to calculate interest rates and investment returns. For example, the return on investment can be calculated using the formula √(principal × rate).

Here's an image to illustrate the concept:

Conclusion

Simplifying square roots is an important mathematical operation that has many real-world applications. By simplifying square roots, we can work with numbers more easily, identify patterns and relationships, and solve equations and problems.

We hope this article has helped you to understand the concept of simplifying square roots and its importance in mathematics and science.

If you have any questions or comments, please feel free to ask.