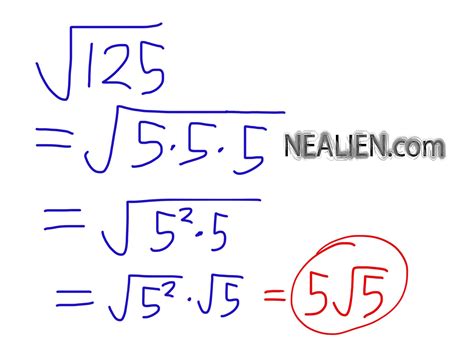Find Square Root Of 125 In Radical Form

Quick Links :

Finding the square root of a number can be a fascinating mathematical journey. In this article, we'll delve into the world of radicals and explore how to find the square root of 125 in its radical form.

Understanding Square Roots

Before we dive into finding the square root of 125, let's quickly review what square roots are. A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4, because 4 multiplied by 4 equals 16.

What is Radical Form?

Radical form is a way of expressing square roots using a radical symbol (√). The radical symbol is used to indicate that we're dealing with a square root. For instance, the square root of 16 can be written in radical form as √16.

Prime Factorization of 125

To find the square root of 125 in radical form, we need to start by finding the prime factorization of 125. Prime factorization involves breaking down a number into its prime factors.

The prime factorization of 125 is:

125 = 5 × 5 × 5

Simplifying the Radical Form

Now that we have the prime factorization of 125, we can simplify the radical form. Since we have three 5's, we can take one 5 out of the radical symbol and leave the other two inside:

√125 = √(5 × 5 × 5) = 5√5

And that's the square root of 125 in radical form!

How to Simplify Radicals

Simplifying radicals involves factoring out perfect squares from the radicand (the number inside the radical symbol). Here are some steps to follow:

• Factor the radicand into its prime factors.
• Identify perfect squares (pairs of identical factors).
• Take one factor from each pair out of the radical symbol.

By following these steps, you can simplify radicals and express them in their simplest form.

Examples of Simplifying Radicals

Here are a few examples to help illustrate the process:

• √48 = √(16 × 3) = 4√3
• √75 = √(25 × 3) = 5√3
• √200 = √(100 × 2) = 10√2

Real-World Applications of Radicals

Radicals have numerous real-world applications in various fields, including:

• Geometry: Radicals are used to find the length of sides in right triangles.
• Trigonometry: Radicals are used to simplify trigonometric expressions.
• Physics: Radicals are used to describe the motion of objects in terms of distance and time.
• Engineering: Radicals are used to design and optimize systems, such as bridges and buildings.

Challenges in Working with Radicals

While radicals can be powerful tools, they can also be challenging to work with. Some common challenges include:

• Simplifying radicals with multiple factors.
• Adding and subtracting radicals with different indices.
• Solving equations involving radicals.

By understanding the basics of radicals and practicing simplification techniques, you can overcome these challenges and become proficient in working with radicals.

Conclusion: Embracing the Power of Radicals

Finding the square root of 125 in radical form may seem like a daunting task, but with the right approach, it can be a rewarding experience. By understanding the basics of radicals, prime factorization, and simplification techniques, you can unlock the power of radicals and tackle even the most complex mathematical challenges.

We invite you to share your thoughts and experiences with radicals in the comments below. How do you use radicals in your daily life or in your studies? What challenges have you faced, and how have you overcome them?