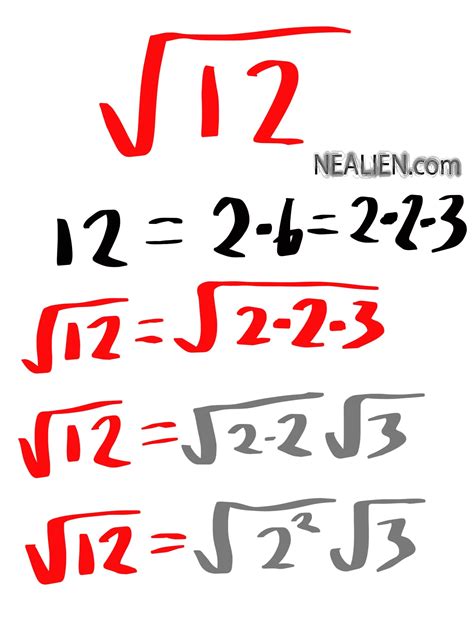The square root of 12 is a mathematical expression that can be simplified in radical form. Understanding how to simplify radicals is an essential skill in mathematics, particularly in algebra and geometry. In this article, we will explore the concept of simplifying the square root of 12 in radical form and provide a step-by-step guide on how to do it.
What is the Square Root of 12?

The square root of 12 is a number that, when multiplied by itself, gives the result of 12. In mathematical notation, it is expressed as √12. The square root of 12 is an irrational number, which means it cannot be expressed as a finite decimal or fraction.
What is Radical Form?

Radical form is a way of expressing numbers that involve square roots. It is a mathematical notation that uses the radical symbol (√) to represent the square root of a number. Radical form is commonly used in algebra and geometry to simplify expressions and solve equations.
Simplifying the Square Root of 12 in Radical Form

To simplify the square root of 12 in radical form, we need to find the largest perfect square that divides 12. A perfect square is a number that can be expressed as the square of an integer, such as 1, 4, 9, or 16. In this case, the largest perfect square that divides 12 is 4.
Using the property of radicals that √ab = √a × √b, we can rewrite √12 as √(4 × 3). Since 4 is a perfect square, we can simplify it further as √4 × √3.
Step-by-Step Simplification
- Identify the largest perfect square that divides 12: 4
- Rewrite √12 as √(4 × 3)
- Simplify √4 as 2
- Rewrite the expression as 2√3
Therefore, the simplified radical form of the square root of 12 is 2√3.
Benefits of Simplifying Radicals

Simplifying radicals has several benefits in mathematics. Some of the advantages include:
- Easier calculations: Simplified radicals make it easier to perform calculations and solve equations.
- Improved accuracy: Simplifying radicals reduces the risk of errors and improves the accuracy of mathematical expressions.
- Enhanced understanding: Simplified radicals provide a clearer understanding of mathematical concepts and relationships.
Real-World Applications of Simplifying Radicals

Simplifying radicals has numerous real-world applications in various fields, including:
- Physics: Simplified radicals are used to calculate distances, velocities, and accelerations in physics problems.
- Engineering: Simplifying radicals is essential in engineering calculations, such as determining the height of a building or the length of a bridge.
- Computer Science: Simplified radicals are used in computer science to optimize algorithms and improve computational efficiency.
Conclusion

In conclusion, simplifying the square root of 12 in radical form is an essential skill in mathematics. By following the step-by-step guide provided in this article, you can simplify the expression √12 as 2√3. Simplifying radicals has numerous benefits and real-world applications in various fields. We hope this article has helped you understand the concept of simplifying radicals and how to apply it in real-world problems.
We invite you to share your thoughts and comments on this article. If you have any questions or need further clarification, please don't hesitate to ask. Share this article with your friends and colleagues who may benefit from this information.
What is the square root of 12?
+The square root of 12 is a number that, when multiplied by itself, gives the result of 12. It is expressed as √12.
What is radical form?
+Radical form is a way of expressing numbers that involve square roots. It uses the radical symbol (√) to represent the square root of a number.
How do you simplify the square root of 12 in radical form?
+To simplify the square root of 12 in radical form, find the largest perfect square that divides 12, which is 4. Rewrite √12 as √(4 × 3), simplify √4 as 2, and rewrite the expression as 2√3.