Square Root Of 11 In Radical Form Simplified

Quick Links :

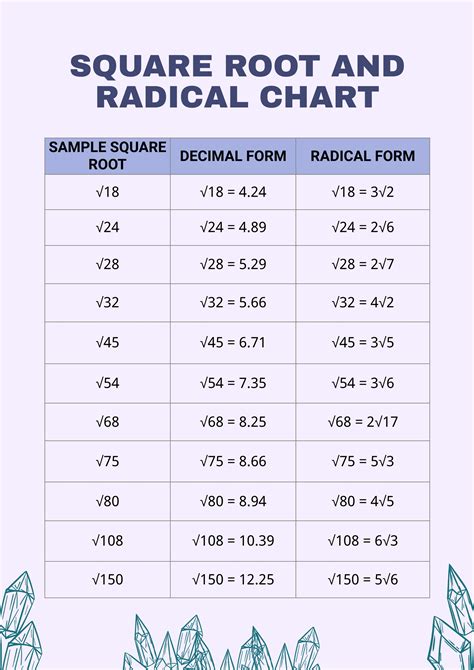
The concept of square roots is a fundamental idea in mathematics, particularly in algebra and geometry. It is essential to understand the basics of square roots to tackle more complex mathematical problems. In this article, we will delve into the concept of square roots, specifically focusing on the square root of 11 in radical form simplified.

What is a Square Root?

A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4, because 4 multiplied by 4 equals 16. The square root symbol is denoted by a radical sign, √, and is usually expressed as √x, where x is the number for which we are finding the square root.

Why Simplify Square Roots?

Simplifying square roots is essential in mathematics, particularly when working with irrational numbers. Irrational numbers are those that cannot be expressed as simple fractions, and their decimal representations go on indefinitely without repeating. Simplifying square roots helps us to express these irrational numbers in a more manageable form.

Square Root of 11 in Radical Form Simplified

To simplify the square root of 11, we need to find the largest perfect square that is a factor of 11. A perfect square is a number that can be expressed as the square of an integer. In this case, the largest perfect square that is a factor of 11 is 1.

Step-by-Step Simplification

Here's a step-by-step guide to simplify the square root of 11:

1. Factor 11 into its prime factors: 11 = 11 × 1
2. Identify the largest perfect square that is a factor of 11: 1
3. Write the square root of 11 as: √11 = √(11 × 1)
4. Simplify the square root by taking the square root of the perfect square factor: √11 = √11 × √1
5. Since the square root of 1 is 1, the simplified form of the square root of 11 is: √11

Why is the Square Root of 11 an Irrational Number?

The square root of 11 is an irrational number because it cannot be expressed as a simple fraction. In other words, there is no integer that, when squared, gives 11. This means that the decimal representation of the square root of 11 goes on indefinitely without repeating.

Practical Applications of Square Roots

Square roots have numerous practical applications in various fields, including:

• Physics and Engineering: Square roots are used to calculate distances, velocities, and accelerations in physics and engineering problems.
• Computer Science: Square roots are used in algorithms for computer graphics, game development, and scientific simulations.
• Finance: Square roots are used in finance to calculate volatility and risk in investment portfolios.

Real-World Examples of Square Roots

Here are some real-world examples of square roots:

• Calculating Distances: In physics, the distance between two points can be calculated using the Pythagorean theorem, which involves square roots.
• Computer Graphics: In computer graphics, square roots are used to calculate the distances between objects in 3D space.
• Investment Analysis: In finance, square roots are used to calculate the volatility of investment portfolios.

Conclusion

In conclusion, the square root of 11 in radical form simplified is √11. Simplifying square roots is essential in mathematics, particularly when working with irrational numbers. The square root of 11 is an irrational number because it cannot be expressed as a simple fraction. Square roots have numerous practical applications in various fields, including physics, engineering, computer science, and finance.

Take Action

If you're interested in learning more about square roots and their applications, we encourage you to explore online resources, such as Khan Academy, MIT OpenCourseWare, or Wolfram Alpha. You can also try solving practice problems on websites like Mathway or Symbolab.

FAQ