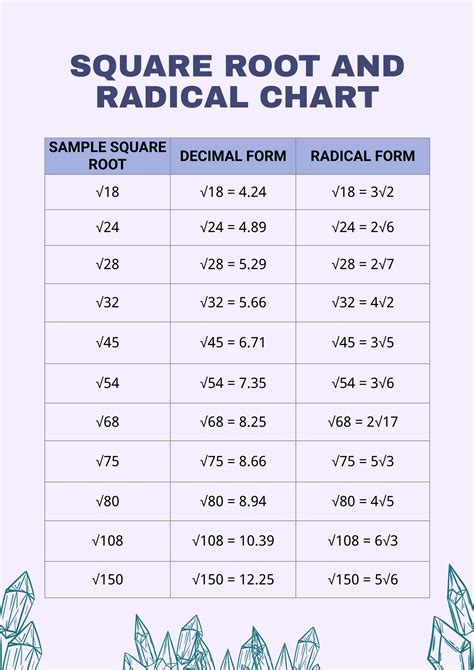
The concept of square roots is a fundamental aspect of mathematics, and understanding how to simplify them is crucial for various mathematical operations. In this article, we will delve into the world of square roots, specifically exploring the square root of 100 in radical form and its simplification.

What is a Square Root?
A square root of a number is a value that, when multiplied by itself, gives the original number. It is denoted by the symbol √. For example, the square root of 16 is 4, because 4 multiplied by 4 equals 16. In mathematical terms, this can be represented as:
√16 = 4
In this case, 4 is the square root of 16.
Radical Form
The radical form of a square root is a way of expressing it using the √ symbol. For instance, the square root of 100 can be written in radical form as:
√100
This notation indicates that we are looking for a number that, when multiplied by itself, gives 100.
Simplifying Square Roots
Simplifying square roots involves finding the most basic form of the radical expression. To simplify a square root, we look for perfect squares that divide evenly into the number inside the radical. A perfect square is a number that can be expressed as the square of an integer, such as 4, 9, 16, or 25.

Example: Simplifying √100
To simplify the square root of 100, we look for perfect squares that divide evenly into 100. The perfect squares that divide 100 are 1, 4, 25, and 100. Among these, 100 is the largest perfect square that divides 100, and its square root is 10.
Therefore, the simplified radical form of √100 is:
10
Why is Simplifying Square Roots Important?
Simplifying square roots is crucial in various mathematical operations, such as solving equations, simplifying expressions, and calculating values. By simplifying square roots, we can:
- Reduce complex expressions to simpler forms
- Solve equations involving square roots
- Calculate values involving square roots

Real-World Applications of Simplifying Square Roots
Simplifying square roots has numerous real-world applications, including:
- Calculating distances and lengths in geometry and trigonometry
- Solving problems involving area and volume in geometry and engineering
- Analyzing data in statistics and data analysis
By simplifying square roots, we can solve complex problems and make accurate calculations in various fields.
Conclusion
In conclusion, simplifying square roots is an essential mathematical concept that helps us reduce complex expressions to simpler forms. By understanding how to simplify square roots, we can solve various mathematical problems and make accurate calculations in real-world applications. The square root of 100 in radical form is √100, which simplifies to 10. This knowledge can be applied to various mathematical operations and real-world problems.

Share Your Thoughts
Do you have any questions or comments about simplifying square roots? Share your thoughts in the comments section below. We'd love to hear from you!

What is the square root of 100 in radical form?
+The square root of 100 in radical form is √100.
How do you simplify the square root of 100?
+To simplify the square root of 100, look for perfect squares that divide evenly into 100. The largest perfect square that divides 100 is 100, and its square root is 10.
Why is simplifying square roots important?
+Simplifying square roots is important because it helps reduce complex expressions to simpler forms, solves equations involving square roots, and calculates values involving square roots.