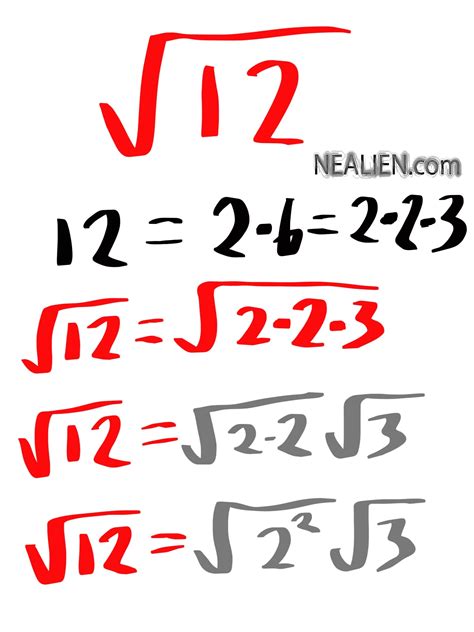Simplifying Square Root 12 In Radical Form

Quick Links :

Simplifying square roots in radical form is an essential concept in mathematics, particularly in algebra and geometry. One of the most common and important square roots to simplify is √12. In this article, we will delve into the world of square roots, explore the concept of simplifying radicals, and provide a step-by-step guide on how to simplify √12 in radical form.

What are Square Roots and Radicals?

Before we dive into simplifying √12, it's essential to understand what square roots and radicals are. A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4, because 4 multiplied by 4 equals 16. The radical symbol √ is used to denote the square root of a number.

Why Simplify Square Roots in Radical Form?

Simplifying square roots in radical form is crucial in mathematics because it helps to:

• Reduce complexity: Simplifying radicals makes it easier to work with mathematical expressions and equations.
• Identify patterns: Simplifying radicals helps to reveal underlying patterns and relationships between numbers.
• Solve equations: Simplifying radicals is essential for solving equations that involve square roots.

How to Simplify √12 in Radical Form

Now that we've covered the basics, let's move on to simplifying √12 in radical form. To simplify √12, we need to find the largest perfect square that divides 12.

Step 1: Factorize 12

To simplify √12, we need to factorize 12 into its prime factors. The prime factorization of 12 is:

12 = 2 × 2 × 3

Step 2: Identify the Largest Perfect Square

Now that we have the prime factorization of 12, we need to identify the largest perfect square that divides 12. In this case, the largest perfect square is 4, which is equal to 2 × 2.

Step 3: Simplify the Radical

Now that we've identified the largest perfect square, we can simplify the radical. We can rewrite √12 as:

√12 = √(4 × 3)

Using the property of radicals that √(ab) = √a × √b, we can simplify further:

√12 = √4 × √3

Step 4: Simplify the Square Root of 4

The square root of 4 is equal to 2, because 2 multiplied by 2 equals 4. Therefore, we can simplify further:

√12 = 2√3

And that's it! We've successfully simplified √12 in radical form.

Benefits of Simplifying Radicals

Simplifying radicals has several benefits, including:

• Improved readability: Simplifying radicals makes mathematical expressions and equations easier to read and understand.
• Increased accuracy: Simplifying radicals reduces the risk of errors and inaccuracies in mathematical calculations.
• Enhanced problem-solving: Simplifying radicals helps to reveal underlying patterns and relationships between numbers, making it easier to solve equations and problems.

Common Mistakes to Avoid When Simplifying Radicals

When simplifying radicals, there are several common mistakes to avoid, including:

• Not factorizing the radicand: Failing to factorize the radicand can lead to incorrect simplifications.
• Not identifying the largest perfect square: Failing to identify the largest perfect square can lead to incomplete simplifications.
• Not simplifying the square root of perfect squares: Failing to simplify the square root of perfect squares can lead to unnecessary complexity.

Real-World Applications of Simplifying Radicals

Simplifying radicals has several real-world applications, including:

• Physics and engineering: Simplifying radicals is essential for solving equations and problems in physics and engineering.
• Computer science: Simplifying radicals is used in computer science to optimize algorithms and improve performance.
• Finance: Simplifying radicals is used in finance to calculate interest rates and investment returns.

Conclusion and Final Thoughts

In conclusion, simplifying √12 in radical form is an essential concept in mathematics that requires a deep understanding of square roots and radicals. By following the steps outlined in this article, you can simplify √12 and other radicals with ease. Remember to avoid common mistakes and appreciate the real-world applications of simplifying radicals.

We hope this article has been informative and helpful. If you have any questions or comments, please feel free to share them below.