Slope-Intercept Form Of A Line Made Easy

Quick Links :

The slope-intercept form of a line is a fundamental concept in algebra and geometry that can seem daunting at first, but with the right approach, it can be made easy to understand and work with. In this article, we will break down the slope-intercept form, explain its benefits, and provide practical examples to help you master this essential math concept.

What is Slope-Intercept Form?

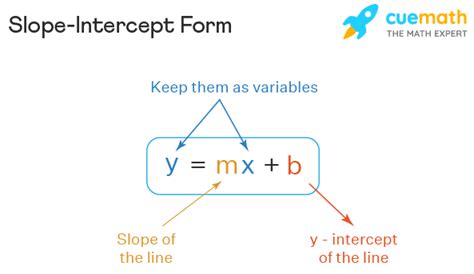
The slope-intercept form of a line is a linear equation that represents a line in the form y = mx + b, where:

• y is the dependent variable (the variable we are trying to solve for)
• m is the slope of the line (a measure of how steep the line is)
• x is the independent variable (the variable we are using to predict the value of y)
• b is the y-intercept (the point where the line intersects the y-axis)

The slope-intercept form is useful because it allows us to easily identify the slope and y-intercept of a line, which can be used to graph the line, find the equation of a line, and solve systems of equations.

Benefits of Slope-Intercept Form

• Easy to graph: With the slope-intercept form, you can easily graph a line by plotting the y-intercept and using the slope to determine the direction and steepness of the line.
• Simple to find the equation: The slope-intercept form makes it easy to find the equation of a line given the slope and y-intercept.
• Useful for solving systems: The slope-intercept form can be used to solve systems of linear equations by equating the slopes and y-intercepts of the two lines.

How to Convert Standard Form to Slope-Intercept Form

Converting a linear equation from standard form (Ax + By = C) to slope-intercept form (y = mx + b) is a straightforward process. Here are the steps:

• Multiply both sides of the equation by -1 to isolate the y variable.
• Divide both sides of the equation by the coefficient of y (B) to solve for y.
• The resulting equation will be in slope-intercept form, with the slope (m) being the coefficient of x and the y-intercept (b) being the constant term.

Example: Converting Standard Form to Slope-Intercept Form

Suppose we have the linear equation 2x + 3y = 6 in standard form. To convert it to slope-intercept form, we follow the steps:

• Multiply both sides of the equation by -1: -2x - 3y = -6
• Divide both sides of the equation by -3: y = (-2/3)x + 2

The resulting equation is in slope-intercept form, with a slope of -2/3 and a y-intercept of 2.

How to Graph a Line in Slope-Intercept Form

Graphing a line in slope-intercept form is a simple process that requires only a few steps:

• Plot the y-intercept (b) on the y-axis.
• Use the slope (m) to determine the direction and steepness of the line.
• Plot a second point on the line by moving up or down from the y-intercept by the slope.
• Draw a line through the two points to complete the graph.

Example: Graphing a Line in Slope-Intercept Form

Suppose we have the linear equation y = 2x + 3 in slope-intercept form. To graph the line, we follow the steps:

• Plot the y-intercept (3) on the y-axis.
• Use the slope (2) to determine the direction and steepness of the line. Since the slope is positive, the line will slope upward from left to right.
• Plot a second point on the line by moving up 2 units from the y-intercept for every 1 unit moved to the right.
• Draw a line through the two points to complete the graph.

Common Applications of Slope-Intercept Form

The slope-intercept form has many practical applications in various fields, including:

• Physics: The slope-intercept form is used to describe the motion of objects under the influence of gravity or other forces.
• Economics: The slope-intercept form is used to model the behavior of markets and the impact of policy changes on economic systems.
• Computer Science: The slope-intercept form is used in computer graphics and game development to create smooth animations and realistic simulations.

Real-World Example: Using Slope-Intercept Form in Physics

Suppose a ball is thrown upward from the ground with an initial velocity of 20 m/s. We can use the slope-intercept form to model the motion of the ball under the influence of gravity.

Let y be the height of the ball above the ground, and x be the time in seconds. The equation of motion can be written in slope-intercept form as:

y = -9.8x + 20

In this equation, the slope (-9.8) represents the acceleration due to gravity, and the y-intercept (20) represents the initial velocity of the ball.

By graphing this equation, we can visualize the motion of the ball and predict its height at any given time.

Conclusion

The slope-intercept form of a line is a powerful tool that can be used to model real-world phenomena, solve systems of equations, and graph linear relationships. By understanding the benefits and applications of slope-intercept form, you can become proficient in using this essential math concept to solve problems and make informed decisions.

We hope this article has helped you to understand the slope-intercept form and its many uses. If you have any questions or comments, please feel free to share them below.