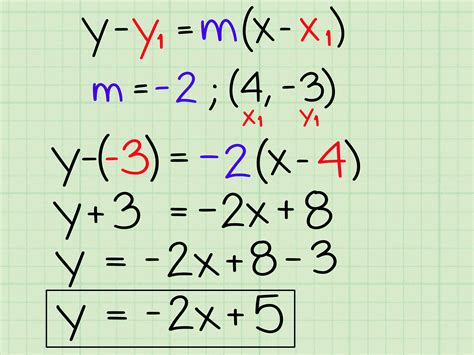Convert 2x 2y 8 To Slope Intercept Form In 2 Steps

Quick Links :

Understanding the concept of linear equations and their various forms is crucial in algebra and other areas of mathematics. The slope-intercept form of a linear equation is one of the most commonly used forms, and it's essential to know how to convert other forms to this format. In this article, we'll explore how to convert the linear equation 2x + 2y = 8 into slope-intercept form in just two steps.

The Importance of Linear Equations

Linear equations are equations in which the highest power of the variable(s) is 1. They can be represented in various forms, including the standard form (ax + by = c), the slope-intercept form (y = mx + b), and the point-slope form (y - y1 = m(x - x1)). Each form has its own advantages and disadvantages, and being able to convert between them is essential for solving problems and graphing lines.

What is Slope-Intercept Form?

The slope-intercept form of a linear equation is y = mx + b, where m represents the slope of the line and b represents the y-intercept. This form is useful for graphing lines, as the y-intercept gives the point where the line crosses the y-axis, and the slope determines the line's steepness and direction.

Step 1: Rearrange the Equation

To convert the given equation 2x + 2y = 8 into slope-intercept form, we need to isolate y on one side of the equation. The first step is to subtract 2x from both sides of the equation:

2x + 2y = 8 2y = -2x + 8

Image:

Step 2: Solve for y

Now that we have 2y = -2x + 8, we can solve for y by dividing both sides of the equation by 2:

2y / 2 = (-2x + 8) / 2 y = -x + 4

Image:

Slope-Intercept Form Achieved!

We've successfully converted the linear equation 2x + 2y = 8 into slope-intercept form, which is y = -x + 4. The slope of the line is -1, indicating a downward slope from left to right. The y-intercept is 4, meaning the line crosses the y-axis at the point (0, 4).

Example Use Cases

The slope-intercept form is useful in various real-world applications, such as:

• Graphing lines on a coordinate plane
• Finding the equation of a line given its slope and y-intercept
• Solving systems of linear equations
• Modeling real-world phenomena, such as the cost of goods or the height of objects

Key Takeaways

• The slope-intercept form of a linear equation is y = mx + b.
• To convert a linear equation to slope-intercept form, isolate y on one side of the equation.
• The slope (m) represents the line's steepness and direction, while the y-intercept (b) gives the point where the line crosses the y-axis.

Encouraging Engagement

Now that you've learned how to convert linear equations to slope-intercept form, try practicing with different equations and exploring the many applications of this concept. Share your thoughts and questions in the comments below, and don't hesitate to ask for help if you need it.

FAQ Section