Convert Radicals To Exponential Form With Ease

Quick Links :

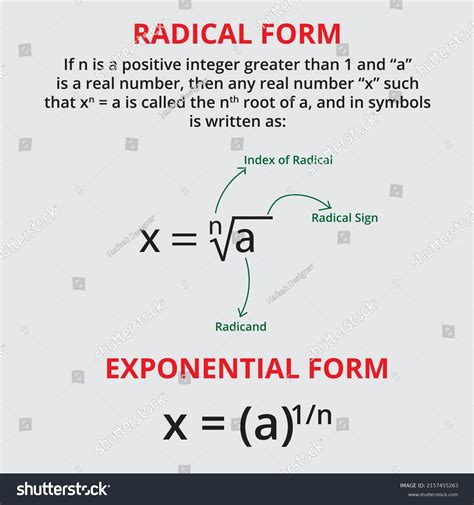
Converting radicals to exponential form is a crucial skill in mathematics, particularly in algebra and calculus. Radicals, also known as roots, can be intimidating, but with the right approach, you can easily convert them to exponential form. In this article, we'll explore the importance of converting radicals to exponential form, the benefits of doing so, and provide step-by-step instructions on how to accomplish this conversion with ease.

Understanding the Importance of Converting Radicals to Exponential Form

Radicals are used to represent numbers that cannot be expressed as simple fractions or decimals. They are commonly used in mathematical operations such as addition, subtraction, multiplication, and division. However, radicals can be challenging to work with, especially when dealing with complex equations or formulas. Converting radicals to exponential form can simplify mathematical expressions and make them easier to manipulate.

Benefits of Converting Radicals to Exponential Form

Converting radicals to exponential form offers several benefits, including:

• Simplified mathematical expressions: Exponential form can simplify complex radical expressions, making them easier to work with.
• Easier calculations: Exponential form can facilitate calculations, such as multiplication and division, by eliminating the need to deal with radicals.
• Improved clarity: Exponential form can provide a clearer representation of mathematical expressions, making it easier to understand and analyze them.

Step-by-Step Instructions for Converting Radicals to Exponential Form

Converting radicals to exponential form involves using the properties of exponents and radicals. Here's a step-by-step guide to help you convert radicals to exponential form with ease:

Step 1: Identify the Radical

Identify the radical expression you want to convert to exponential form. For example, √x or ³√x.

Step 2: Determine the Index

Determine the index of the radical. The index is the small number outside the radical symbol, which indicates the root of the number. For example, in √x, the index is 2.

Step 3: Apply the Exponent Rule

Apply the exponent rule, which states that a^(1/n) = nth root of a. For example, √x = x^(1/2) or ³√x = x^(1/3).

Step 4: Simplify the Expression

Simplify the expression by combining any like terms or applying any additional exponent rules.

Examples of Converting Radicals to Exponential Form

Here are a few examples to illustrate the process of converting radicals to exponential form:

• √x = x^(1/2)
• ³√x = x^(1/3)
• ⁴√x = x^(1/4)
• √(x^2) = x^(2/2) = x^1 = x

Common Mistakes to Avoid When Converting Radicals to Exponential Form

When converting radicals to exponential form, it's essential to avoid common mistakes that can lead to errors. Here are a few mistakes to watch out for:

• Forgetting to apply the exponent rule correctly
• Failing to simplify the expression
• Confusing the index of the radical with the exponent

Practical Applications of Converting Radicals to Exponential Form

Converting radicals to exponential form has numerous practical applications in mathematics, science, and engineering. Here are a few examples:

• Simplifying complex equations in physics and engineering
• Analyzing mathematical expressions in calculus and algebra
• Solving problems in computer science and programming

Conclusion and Final Thoughts

Converting radicals to exponential form is a valuable skill that can simplify mathematical expressions and make them easier to work with. By following the step-by-step instructions outlined in this article, you can master the art of converting radicals to exponential form with ease. Remember to avoid common mistakes and practice, practice, practice to become proficient in this skill.

We hope this article has been informative and helpful in your journey to learn about converting radicals to exponential form. If you have any questions or need further clarification, please don't hesitate to comment below.