Convert Radicals To Exponential Form In 3 Easy Steps

Quick Links :

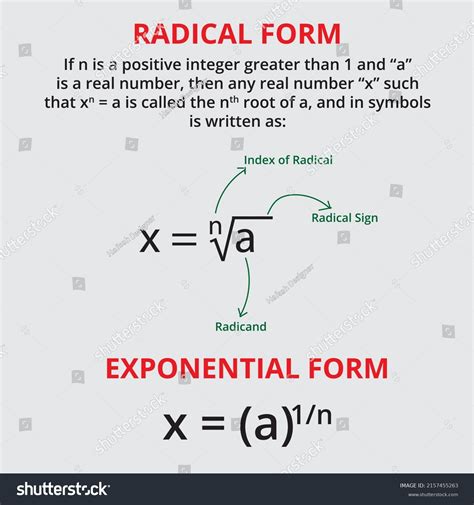
Radicals and exponents are two fundamental concepts in mathematics that can be used to represent and manipulate expressions. While they may seem like two different entities, radicals can be converted to exponential form, making it easier to perform calculations and simplify expressions. In this article, we will explore the process of converting radicals to exponential form in three easy steps.

Radicals are mathematical expressions that contain a root symbol (√), indicating the operation of finding the root of a number. On the other hand, exponents are mathematical expressions that represent repeated multiplication of a number. For instance, the expression 2^3 represents 2 multiplied by itself three times (2 × 2 × 2). By converting radicals to exponential form, we can take advantage of the properties of exponents to simplify expressions and make calculations more efficient.

Step 1: Identify the Type of Radical

The first step in converting radicals to exponential form is to identify the type of radical. There are two main types of radicals: square roots (√) and nth roots (ⁿ√). Square roots are used to find the number that, when multiplied by itself, gives the original number. For example, √16 = 4 because 4 × 4 = 16. Nth roots, on the other hand, are used to find the number that, when raised to the power of n, gives the original number. For instance, ³√27 = 3 because 3³ = 27.

Understanding the Concept of Exponents

Before we proceed with the conversion process, it's essential to understand the concept of exponents. Exponents are shorthand notation for repeated multiplication. For example, 2^3 represents 2 multiplied by itself three times (2 × 2 × 2). Exponents can also be used to represent roots. For instance, ²√16 can be written as 16^(1/2), which is equivalent to 4.

Step 2: Convert the Radical to Exponential Form

Once we have identified the type of radical, the next step is to convert it to exponential form. To do this, we use the following rules:

• Square roots (√) can be converted to exponential form by raising the number to the power of 1/2. For example, √16 = 16^(1/2)
• Nth roots (ⁿ√) can be converted to exponential form by raising the number to the power of 1/n. For instance, ³√27 = 27^(1/3)

Step 3: Simplify the Exponential Expression

The final step is to simplify the exponential expression. This can be done by using the properties of exponents, such as multiplying exponents with the same base or combining exponents with different bases.

For example, let's simplify the expression 16^(1/2) + 27^(1/3). We can start by evaluating the exponents:

16^(1/2) = √16 = 4 27^(1/3) = ³√27 = 3

Then, we can add the results:

4 + 3 = 7

Therefore, the simplified expression is 7.

Benefits of Converting Radicals to Exponential Form

Converting radicals to exponential form has several benefits, including:

• Simplifying Expressions: Exponential form can be used to simplify complex expressions involving radicals.
• Easier Calculations: Exponential form makes it easier to perform calculations, such as multiplying and dividing expressions.
• Improved Readability: Exponential form can make expressions more readable and easier to understand.

Common Applications of Converting Radicals to Exponential Form

Converting radicals to exponential form has numerous applications in various fields, including:

• Algebra: Exponential form is used to simplify expressions and solve equations.
• Geometry: Exponential form is used to calculate distances and volumes.
• Trigonometry: Exponential form is used to simplify trigonometric expressions and solve equations.

Conclusion

In conclusion, converting radicals to exponential form is a simple process that can be done in three easy steps. By understanding the concept of exponents and using the rules for converting radicals to exponential form, we can simplify expressions and make calculations more efficient. Whether you're a student or a professional, mastering the art of converting radicals to exponential form can help you solve complex problems and achieve your goals.