4 Ways To Master Quadratic X-Intercept Form

Quick Links :

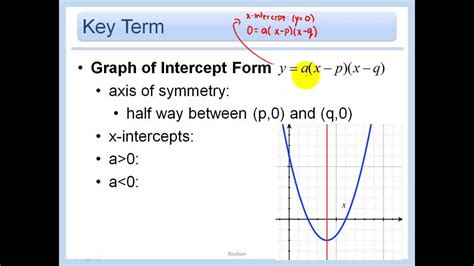
Understanding quadratic equations and their various forms is crucial in algebra and mathematics as a whole. Among these forms, the X-intercept form, also known as the factored form, is particularly useful for solving quadratic equations and graphing parabolas. The standard form of a quadratic equation is ax^2 + bx + c = 0, but when we're looking at the X-intercept form, we're dealing with equations in the form of a(x - p)(x - q) = 0, where p and q are the x-intercepts of the parabola.

What is Quadratic X-Intercept Form?

In the X-intercept form, the equation is written in a way that directly shows the x-intercepts (or roots) of the quadratic equation. This form is especially helpful when we need to quickly identify the points where the graph of the parabola crosses the x-axis.

Why is Quadratic X-Intercept Form Important?

Understanding and working with the X-intercept form can simplify the process of graphing quadratic equations and solving problems related to these equations. Here are a few reasons why mastering this form is beneficial:

• Easy Graphing: Knowing the x-intercepts makes it easier to graph the parabola since these points are where the graph intersects the x-axis.
• Solving Quadratic Equations: The X-intercept form makes solving quadratic equations straightforward because it directly provides the roots of the equation.
• Identifying Key Features: It helps in identifying key features of the parabola, such as its vertex, axis of symmetry, and the direction it opens.

How to Master Quadratic X-Intercept Form in 4 Steps

Step 1: Understand the Basics

To start mastering the X-intercept form, you need to understand the basics of quadratic equations and how they are represented in this form. Familiarize yourself with the general form a(x - p)(x - q) = 0 and understand that p and q represent the x-intercepts of the graph.

Step 2: Learn to Factor

Factoring is a critical skill for working with the X-intercept form. Practice factoring quadratic expressions into their X-intercept form. This involves identifying two numbers (p and q) whose product is c/a and whose sum is b/a. Once you can factor expressions into this form, you'll be able to find the x-intercepts of any quadratic equation.

Step 3: Practice Graphing

Graphing is a key aspect of mastering quadratic equations in X-intercept form. After identifying the x-intercepts, practice plotting these points on a coordinate plane and drawing the parabola. Remember, the vertex form (a(x - h)^2 + k) can also be helpful for graphing, but knowing the x-intercepts gives you a solid starting point.

Step 4: Apply to Real-World Problems

Finally, apply your knowledge of the X-intercept form to real-world problems. Quadratic equations appear in physics, engineering, economics, and more. By mastering the X-intercept form, you'll be able to model and solve problems more efficiently.

Common Challenges and Solutions

Challenge 1: Difficulty in Factoring

Some quadratic expressions are harder to factor than others. If you're having trouble factoring an expression, try using the quadratic formula to find the roots. Once you have the roots, you can write the expression in X-intercept form.

Challenge 2: Identifying X-Intercepts

Always remember that the x-intercepts are the points where the graph crosses the x-axis. If you're having trouble identifying these points, try graphing the parabola or using the quadratic formula.

Challenge 3: Applying to Complex Problems

Applying the X-intercept form to complex problems can be overwhelming. Start by breaking down the problem into simpler parts. Identify the quadratic equation involved, and then apply your knowledge of the X-intercept form to solve it.

Conclusion: Mastering Quadratic X-Intercept Form for Success

Mastering the quadratic X-intercept form is a valuable skill that can simplify your work with quadratic equations and enhance your problem-solving abilities. By following the steps outlined above and practicing regularly, you'll become proficient in using this form to solve a variety of problems. Remember, practice is key, so continue to challenge yourself with different types of quadratic equations and applications.

We invite you to share your thoughts, ask questions, or discuss your own experiences with mastering the quadratic X-intercept form. Your engagement will help create a valuable resource for everyone interested in this topic.