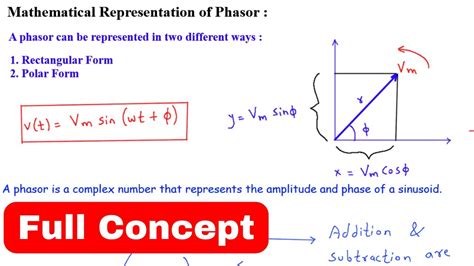
The debate between polar form and rectangular form has been ongoing for a long time in the mathematical community. While both forms have their own advantages and disadvantages, polar form is often considered the more practical and efficient choice. Here are five ways polar form beats rectangular form:
Working with polar form can simplify complex calculations and provide a more intuitive understanding of mathematical concepts. By utilizing polar coordinates, mathematicians and engineers can better comprehend the relationships between different components of a vector or a complex number. This can lead to a deeper understanding of the underlying principles and a more efficient approach to problem-solving.
1. Easier Trigonometric Calculations

One of the most significant advantages of polar form is its ability to simplify trigonometric calculations. When working with polar coordinates, mathematicians can easily express complex trigonometric functions in terms of their magnitude and direction. This allows for faster and more accurate calculations, making polar form an essential tool for many mathematical applications.
For example, when calculating the sine or cosine of a complex number in rectangular form, mathematicians must use the Pythagorean theorem to determine the magnitude of the number and then apply the trigonometric function. In contrast, polar form allows for a more straightforward approach, using the magnitude and direction of the complex number to calculate the trigonometric function directly.
Benefits of Polar Form Trigonometry
• Simplifies complex trigonometric calculations • Reduces error-prone steps • Enhances understanding of mathematical concepts
2. Improved Visualization and Intuition

Polar form provides a more intuitive and visual representation of mathematical concepts, allowing mathematicians and engineers to better understand the relationships between different components of a vector or a complex number. By expressing complex numbers in terms of their magnitude and direction, polar form provides a clear and concise picture of the underlying mathematics.
This improved visualization and intuition enable mathematicians to make more accurate predictions and interpretations of mathematical data. In fields such as engineering, physics, and navigation, polar form is essential for understanding complex systems and making precise calculations.
Benefits of Polar Form Visualization
• Enhances understanding of mathematical concepts • Provides a clear and concise picture of complex numbers • Facilitates more accurate predictions and interpretations
3. Efficient Representation of Complex Numbers

Polar form provides an efficient and compact representation of complex numbers, making it easier to store and manipulate mathematical data. By expressing complex numbers in terms of their magnitude and direction, polar form reduces the amount of data required to represent a complex number, making it more efficient for computational applications.
This efficient representation also facilitates faster calculations, as mathematicians can quickly determine the magnitude and direction of a complex number without having to perform unnecessary calculations. In fields such as computer science and electrical engineering, polar form is essential for efficient data representation and calculations.
Benefits of Polar Form Complex Numbers
• Reduces data required to represent complex numbers • Facilitates faster calculations • Enhances efficiency in computational applications
4. Simplified Calculations for Multiplication and Division

Polar form simplifies calculations for multiplication and division of complex numbers, making it a more efficient and practical choice for many mathematical applications. By expressing complex numbers in terms of their magnitude and direction, polar form allows for a more straightforward approach to multiplication and division.
For example, when multiplying two complex numbers in rectangular form, mathematicians must use the distributive property and FOIL method to calculate the product. In contrast, polar form allows for a more straightforward approach, using the magnitude and direction of the complex numbers to calculate the product directly.
Benefits of Polar Form Multiplication and Division
• Simplifies calculations for multiplication and division • Reduces error-prone steps • Enhances efficiency in mathematical applications
5. Enhanced Understanding of Mathematical Concepts

Polar form provides a deeper understanding of mathematical concepts, allowing mathematicians and engineers to better comprehend the underlying principles and relationships between different components of a vector or a complex number. By expressing complex numbers in terms of their magnitude and direction, polar form enables mathematicians to visualize and interpret mathematical data more effectively.
This enhanced understanding of mathematical concepts enables mathematicians to make more accurate predictions and interpretations of mathematical data, leading to breakthroughs in various fields of science and engineering.
Benefits of Polar Form Mathematical Concepts
• Enhances understanding of mathematical concepts • Facilitates more accurate predictions and interpretations • Leads to breakthroughs in various fields of science and engineering
In conclusion, polar form offers several advantages over rectangular form, including easier trigonometric calculations, improved visualization and intuition, efficient representation of complex numbers, simplified calculations for multiplication and division, and enhanced understanding of mathematical concepts. By utilizing polar form, mathematicians and engineers can simplify complex calculations, gain a deeper understanding of mathematical concepts, and make more accurate predictions and interpretations of mathematical data.
We'd love to hear from you! Share your thoughts on the benefits of polar form and how it has helped you in your mathematical endeavors. Leave a comment below and let's discuss!